Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROSTATICS - I
MOTION|Exercise EXERCISE - 1 (Section A)|10 VideosELECTROSTATICS - I
MOTION|Exercise EXERCISE - 1 (Section B)|10 VideosELECTROSTATICS
MOTION|Exercise Exercise -3 Section (B) Previous Year Problems | JEE Main|30 VideosELECTROSTATICS-II
MOTION|Exercise Exercise - 4 (Level - II)|30 Videos
MOTION-ELECTROSTATICS - I -EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
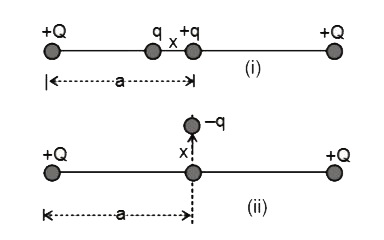
- Two small particles charged with equal positive charges Q each, are fi...
Text Solution
|
- Poistive and negative point charges of equal magnitude are kept at (0,...
Text Solution
|
- Conisder a system of three charges q//3, q//3 and -2q//3 placed at poi...
Text Solution
|
- A few electric field lines for a system of two charges Q1 and Q2 fixed...
Text Solution
|
- Under the influence of the Coulomb field of charge +Q, a charge -q is ...
Text Solution
|
- A tiny spherical oil drop carrying a net charge q is balanced in still...
Text Solution
|
- Four point charges, each of +q, are rigidly fixed at the four corners ...
Text Solution
|
- A wooden block performs SHM on a frictionaless surface with frequency,...
Text Solution
|
- Two large vertical and parallel metal plates having a separation of 1c...
Text Solution
|
- Conisder a thin spherical shell of radius R with centre at the origin,...
Text Solution
|
- Six point charges are kept at the vertices of a regular hexagon of sid...
Text Solution
|
- Four charges Q(1), Q(2), Q(3) and Q(4) of same magnitude are fixed alo...
Text Solution
|
- The electric field is measured at a point 0,0, generated due to vario...
Text Solution
|
- A dipole of Dipole moment vec(p)=(p(0))/(sqrt(2))(hat(i)+hat(j)). Is p...
Text Solution
|