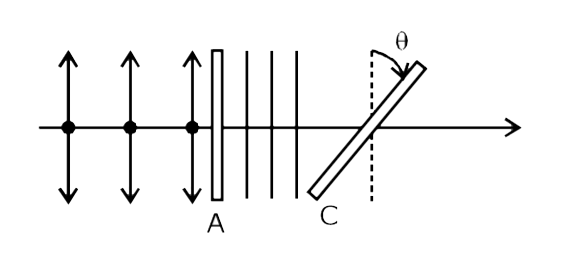
Text Solution
Verified by Experts
Recommended Questions
- Two crossed polarod A and B are placed in the path of a beam of unpola...
Text Solution
|
- At what angle should the axes of two polaroids be placed so as to redu...
Text Solution
|
- The polaroids are placed in the path of unpolarized beam of intensity ...
Text Solution
|
- Two crossed polarod A and B are placed in the path of a beam of unpola...
Text Solution
|
- Two polaroids with their principal sections aligned at 60^@ , are plac...
Text Solution
|
- Two polaroids A and B are parallel. How a third Polaroid C be placed b...
Text Solution
|
- Two 'crossed' polaroids A and B are placed in the path of a light-beam...
Text Solution
|
- Two polaroids are placed in the path of unpolarised light beam of inte...
Text Solution
|
- Two polaroids are placed in the path of unpolarised light of intensity...
Text Solution
|