Text Solution
Verified by Experts
Topper's Solved these Questions
FRICTION AND CIRCULAR MOTION
GRB PUBLICATION|Exercise Problem For Practice|23 VideosFRICTION AND CIRCULAR MOTION
GRB PUBLICATION|Exercise OBJECTIVE QUESTIONS ( only one choice is correct )|80 VideosFORCE AND NEWTONS LAWS OF MOTION
GRB PUBLICATION|Exercise Comprehension|12 VideosMOTION IN A STRAIGHT LINE
GRB PUBLICATION|Exercise Comprehension type Queston|14 Videos
Similar Questions
Explore conceptually related problems
GRB PUBLICATION-FRICTION AND CIRCULAR MOTION -Comprehension type
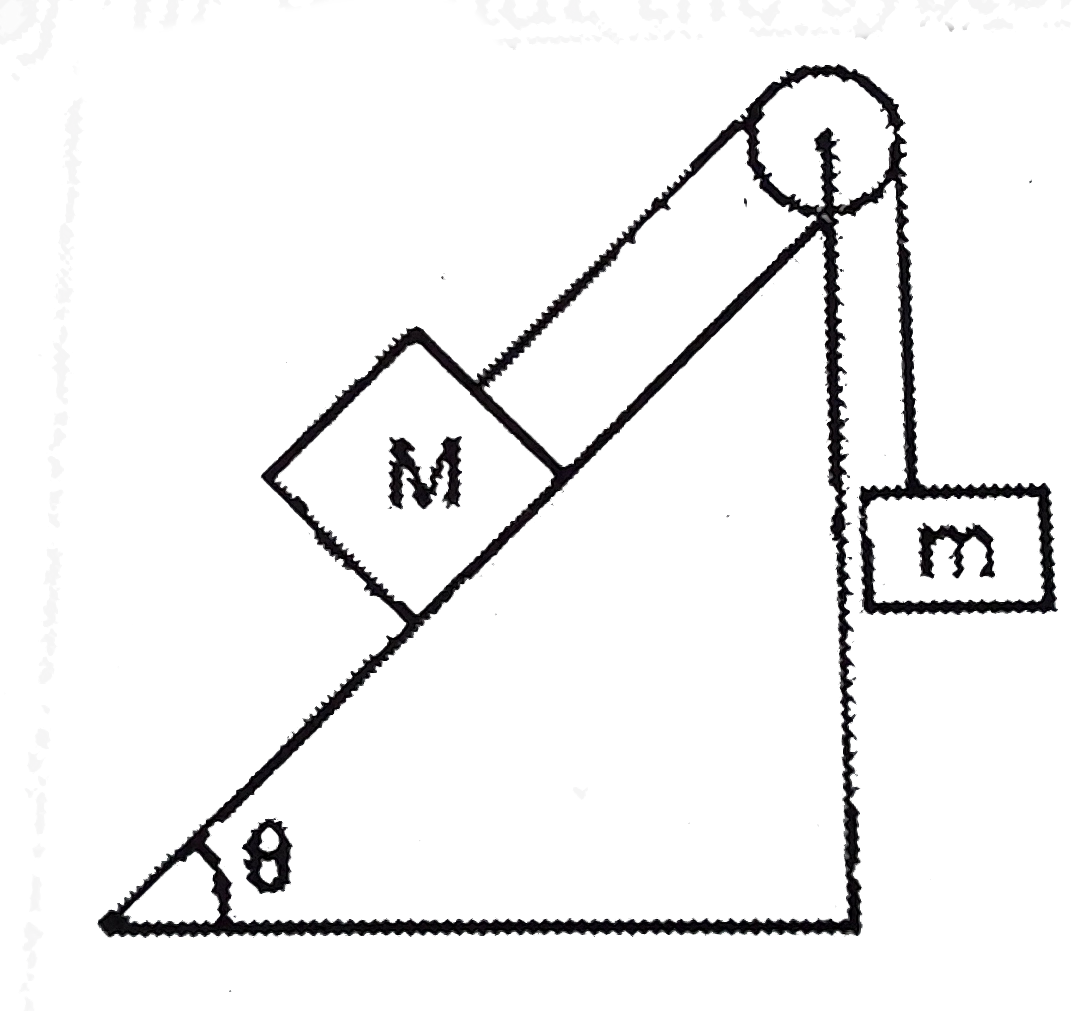
- Two blocks of mass m and M, are connect to the ends of a string passin...
Text Solution
|
- When F = 2 N , the frictional force between 5 kg block and ground is :
Text Solution
|
- The acceleration of 10 kg block when F = 30 N ,
Text Solution
|
- Find the minimum value of F for which 5 kg being to slide if the coeff...
Text Solution
|
- Two bodies A and B of masses 10 kg and 5 kg are placed very slightly s...
Text Solution
|
- Two bodies A and B of masses 10 kg and 5 kg are placed very slightly s...
Text Solution
|
- Two bodies A and B of masses 10 kg and 5 kg are placed very slightly s...
Text Solution
|
- A block of mass M slides on a frictionless surface with an initial spe...
Text Solution
|
- A block of mass M slides on a frictionless surface with an initial spe...
Text Solution
|
- A block of mass M slides on a frictionless surface with an initial spe...
Text Solution
|
- A frame of reference that is accelerated with respect to an inertial f...
Text Solution
|
- A frame of reference that is accelerated with respect to an inertial f...
Text Solution
|