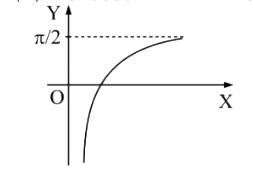
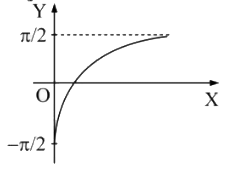
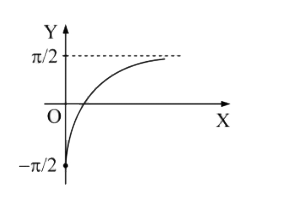
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- f: (0,oo) to (-pi/2,pi/2)" be defined as, "f(x)=tan^(-1) (log(e)x). ...
Text Solution
|
- If f(x)=sin x+tan x-2x, where f:[0,(pi)/(2)]rarr(0,oo), then
Text Solution
|
- Consider f:(0,oo)rarr(-(pi)/(2),(pi)/(2)), defined as f(x)=tan^(-1)((l...
Text Solution
|
- f:(-(pi)/(2),(pi)/(2))rarr(-oo,oo) defined by f(x)=tan x is
Text Solution
|
- If f:(-(pi)/(2),(pi)/(2))rarr(-oo,oo) is defined by f(x)=tan x then f^...
Text Solution
|
- Let the function f(x) = tan^(1-) (sin x + cos x) be defined on [ 0, 2 ...
Text Solution
|
- If f'(x) = tan^(-1)(Sec x + tan x), x in (-pi/2 , pi/2) and f(0) = 0 t...
Text Solution
|
- If f(x)=(e^(x)+e^(-x)-2)/(x sin x), for x in [(-pi)/(2), (pi)/(2)]-{0}...
Text Solution
|
- The function f(x)=tan x" for "x ne pi//2, f(pi//2)=0" at "x=pi//2" is ...
Text Solution
|