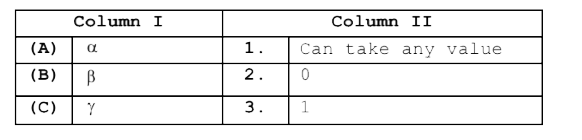Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let P (alpha, beta, gamma) and Q(1,-1,0) be points such that the mid-p...
Text Solution
|
- If alpha,beta,gamma are the cube roots of p, then for any x,y,z (x al...
Text Solution
|
- If alpha,beta,gamma are cube roots of of p<0 then for any real x,y,z;(...
Text Solution
|
- If alpha,beta,gamma are the cube roots of p then for any x,y and z(x a...
Text Solution
|
- If y=1/(1+x^(beta-alpha)+x^(gamma-alpha))+1/(1+x^(alpha-beta)+x^(gamma...
Text Solution
|
- Let x-y sin alpha-z sin beta=0;x sin alpha-y+z sin gamma=0 and x sin b...
Text Solution
|
- Prove that |{:(1,x+alpha,y+z-alpha),(1,t+beta,+x-beta),(1,z+gamma,x...
Text Solution
|
- A line makes angles alpha, beta, gamma with X, Y, Z axes respectively....
Text Solution
|
- A line makes angles alpha, beta, gamma with X, Y, Z axes respectively....
Text Solution
|