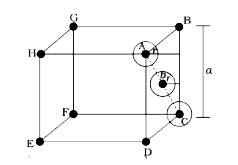
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A metal crystallises in a face centred cubic structure. If the edge le...
Text Solution
|
- A metal crystallises in a face centred cubic structure. If the edge le...
Text Solution
|
- Metallic gold crystallises in face centred cubic lattice with edge-len...
Text Solution
|
- A metal crystallises in a face centred cubic structure. If the edge le...
Text Solution
|
- A metal crystallises in a face centred cubic structure. If the edge le...
Text Solution
|
- A metal crystallises in a face centred cubic structure. If the edge le...
Text Solution
|
- A metal crystallises in a face centred cubic structure. If the edge le...
Text Solution
|
- A metal crystallises in a face-centred cubic structure. If the edge le...
Text Solution
|
- A metal crystallises in a face centred cubic structure . If the edge l...
Text Solution
|