A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
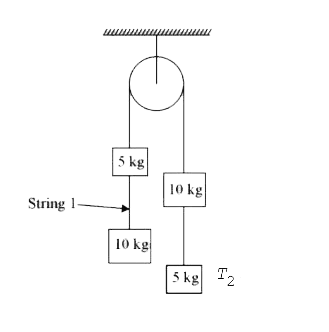
- Find the value of tension in string 1 if the system equilibrium ? (...
Text Solution
|
- A ball of mass 1 kg hangs in equilibrium from two string OA and OB as ...
Text Solution
|
- In given arrangement, 10 kg and 20 kg blocks are kept at rest on two f...
Text Solution
|
- If tension in string A and string B are T(A) and T(B) then find out (T...
Text Solution
|
- चित्र में दिखाई गई स्थिति में डोरी में तनाव की गणना करें | डोरी भारहीन...
Text Solution
|
- A mass of 2 kg tied to a string 1 m length is rotate in a verticle cir...
Text Solution
|
- The system shown in figure is in equilibrium. Find the magnitude of te...
Text Solution
|
- A 10 kg steel ball is suspended by two strings as shown. The tensions ...
Text Solution
|
- Find the value of tension in string 1 if the system equilibrium ? (g=1...
Text Solution
|