Home
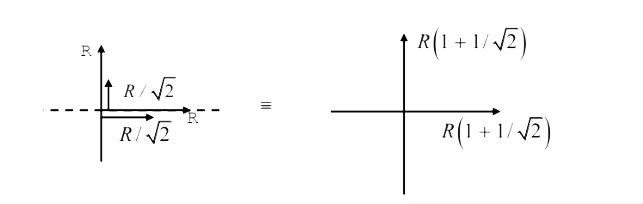
Class 12
PHYSICS
Find the resultant of the three vectors ...

Find the resultant of the three vectors `vec(OA), vec(OB)` and `vec(OC)` shown in figure. Radius of the circle is R.

A

2R

B

`R(1+sqrt(2))`

C

`Rsqrt(2)`

D

`R(sqrt(2)-1)`

Text Solution

Verified by Experts

The correct Answer is:
b

`rarr` magnitude of resultant is `sqrt(R^(2)(1+(1)/sqrt(2)^(2))+R^(2)(1+(1)/sqrt(2)^(2))=R(1+sqrt(2))`
Promotional Banner

Similar Questions

Explore conceptually related problems

The resultant of the three vectors vec(OA), vec(OB) and vec(OC) shown in figure is

Find the resultant of the three vectors vec OA,vec OB and vec OC each of magnitude r as shown in figure?

What is the angle between the vector vec(A) and vec(B) as shown in figure ?

The resultant of vectors vec(OA) and vec(OB) is peerpendicular to vec(OA). Find the angle AOB.

The magnitude of vectors vec(OA), vec(OB) and vec (OC) in figure are equal. Find the direction of vec(OA)+vec(OB)-vec(OC) . .

The resultant of two velocity vectors vec(A) and vec(B) is perpendicular to vec(A) . Magnitude of Resultant vec(R ) is equal to half magnitude of vec(B) . If the angle between vec(A) and vec(B) is (30 theta)^(@) , then value of theta is ?

The resultant of two vectors vec(A) and vec(B) is perpendicular to the vector vec(A) and its magnitudes is equal to half of the magnitudes of vector vec(B) (figure). The angle between vec(A) and vec(B) is

The magnitudes of vectors vec OA,vec OB and vec OC( in figure( 2-W3) are equal.Find the direction of )/(Ovec A)+vec OB-vec OC.

The sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors vec(OB) and vec(OC) .

ABCD is a quadrilateral and E is the point of intersection of the lines joining the middle points of opposite side. Show that the resultant of vec (OA) , vec(OB) , vec(OC) and vec(OD) = 4 vec(OE) , where O is any point.