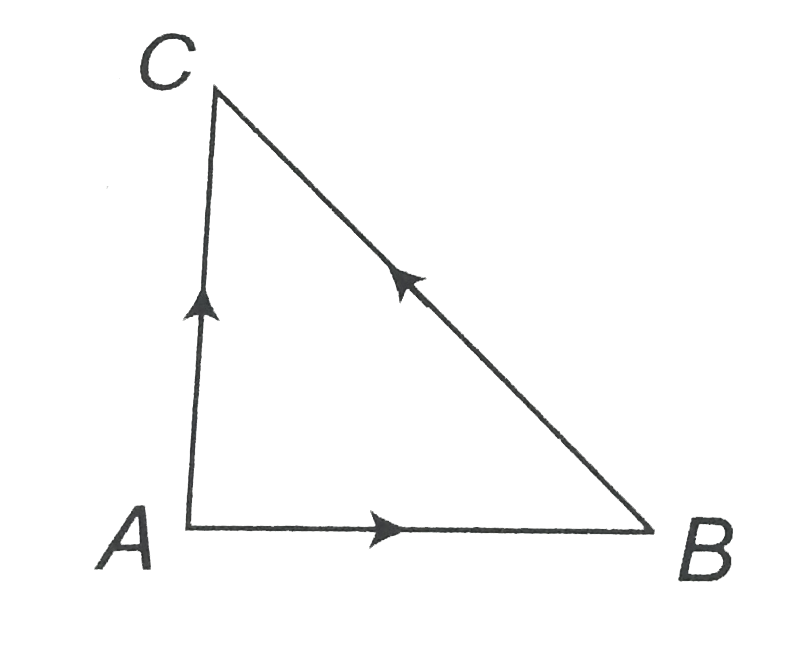
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Three forces start acting simultaneously on a particle moving with vel...
Text Solution
|
- Three forces start acting simultaneously on a particle moving with vel...
Text Solution
|
- A particle moving with velocity vecV is acted by the three forces show...
Text Solution
|
- Three forces start acting simultaneously on a particle moving the velo...
Text Solution
|
- Three forces start acting simultaneously on a particle moving with vel...
Text Solution
|
- तीन बल vecv वेग से चलने वाले कण पर एक साथ कार्य करते हैं । इन बलों के ...
Text Solution
|
- Three forces start acting simultaneously on a particle , moving with v...
Text Solution
|
- सदिश त्रिभुज PQR में दर्शाए अनुसार वेग vecV से गतिमान किसी कण पर तीन ब...
Text Solution
|
- Three forcesstart acting simultaneously on a particle moving with a ve...
Text Solution
|