Text Solution
Verified by Experts
Topper's Solved these Questions
CURRENT ELECTRICITY
MOTION|Exercise EXERCISE -1 (SECTION -A Definition of Current , Current Density , Drift Velocity )|8 VideosCURRENT ELECTRICITY
MOTION|Exercise EXERCISE -1(SECTION B- Resistance & resistivity , Ohms law +VI (Volt - curr.) Characteristics + Colour Code + Temp . Dependence|8 VideosCURRENT ELECTRICITY
MOTION|Exercise EXERCISE -3 SECTION -B (PREVIOUS YEAR PROBLEMS JEE MAIN)|42 VideosCONSTRAINED MOTION
MOTION|Exercise EXAMPLES|12 VideosELASTICITY
MOTION|Exercise EXERCISE -3|60 Videos
Similar Questions
Explore conceptually related problems
MOTION-CURRENT ELECTRICITY-EXAMPLE
- The dimensions of a conductor of specific resistance p are shown. Find...
Text Solution
|
- A portion of length L is cut out of a conical solid wire the two ends ...
Text Solution
|
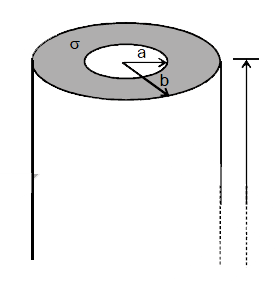
- The space between two coaxial cylinders, whose radii are a and b (wher...
Text Solution
|
- Find V(A)-V(B)
Text Solution
|
- Shown in the figure . Find out the current in the wire BD
Text Solution
|
- Find the current in each wire
Text Solution
|
- Find the potential at point A
Text Solution
|
- Find the current in every branch ?
Text Solution
|
- Find the current in every branch ?
Text Solution
|
- Find the current in every branch ?
Text Solution
|
- Find current in the circuit
Text Solution
|
- Find the current in each wire applying only Kirchhoff voltage law
Text Solution
|
- Find current which is passing through battery .
Text Solution
|
- Find equivalent Resistance
Text Solution
|
- Find the current in Resistance P if voltage supply between A and B vol...
Text Solution
|
- Find the current in 2 Omega resistance.
Text Solution
|
- In the circuit shown in figure . (a) find the current flowing through ...
Text Solution
|
- Find equivalent resistance of the circuit between the terminals A and ...
Text Solution
|
- Find the equivalent resistance between a and B
Text Solution
|
- Find equivalent resistance ?
Text Solution
|