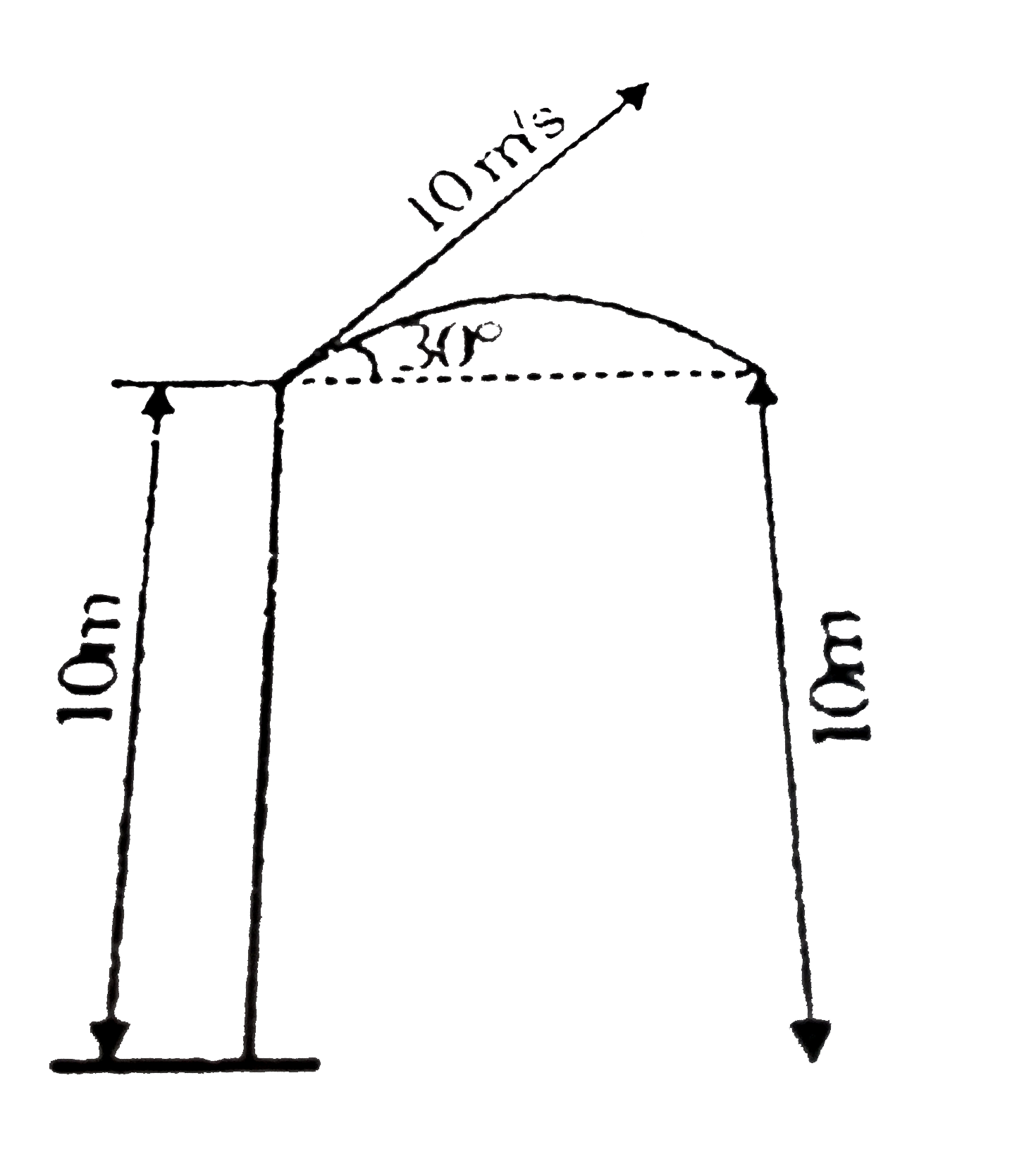
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A boat man can row with a speed of 10 km/hr in still water. The river...
Text Solution
|
- A boat is rowed across a river at the rate of 4.5(km)/(hr). The river ...
Text Solution
|
- A river is flowing steradily with a speed 5 km h^(-1) . A boat man ca...
Text Solution
|
- A man travels by boat 36 km down a river and back in 8 hours. If the s...
Text Solution
|
- A boat which has a speed of 5 km/hr in still water crosses a river of ...
Text Solution
|
- If a boat can have a speed of 4 km/hr in still water, for what values ...
Text Solution
|
- The width of a river is 2sqrt(3) km. A boat is rowed in direction perp...
Text Solution
|
- एक नाविक शांत पानी में 10 km/h की चाल से नाव चला सकता है। यदि नदी 5 km...
Text Solution
|
- A river flows at the rate of 3 km/hr and a person can row a boat at a ...
Text Solution
|