Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
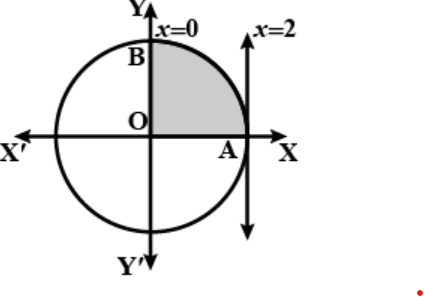
- Area lying in the first quadrant and bounded by the circle x^2+y^2=4 ...
Text Solution
|
- Area lying in the first quadrant and bounded by the circle x^2+y^2=4 ...
Text Solution
|
- The area bounded by the curves x^(2)+y^(2)=1,x^(2)+y^(2)=4 and the pai...
Text Solution
|
- Area lying in the first quadrant and bounded by the circle x^(2) +y ^(...
Text Solution
|
- Area lying in the first quadrant and bounded by the circle x ^(2) +y ^...
Text Solution
|
- Area lying in the first quadrant and bounded by the circle x^(2) + y^(...
Text Solution
|
- Area lying in the first quadrant and bounded by the circle x^(2) + y^(...
Text Solution
|
- Area lying in the first quadrant and bounded by the circle x^(2) + y^(...
Text Solution
|
- The area bounded by the curves x^2+y^2=1,x^2+y^2=4 and the pair of lin...
Text Solution
|