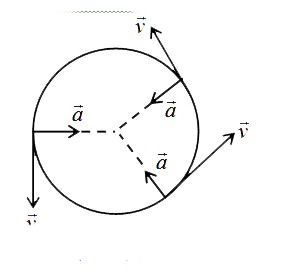When an object moves in a circular path with constant speed, the direction of velocity changes at every point in its path, due to which an acceleration will be produced towards the centre of the circle which is called centripetal acceleration. Let, m-mass of the particle, v-constant speed, `omega` uniform angular speed, r-radius of the circular path
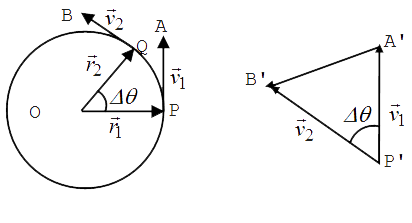
At any time t, the particle is at P with position vector `overset(-)(OP)=vecr_(1)" and at time " t+trianglet` the particle is at Q with position vector `overset(-)(OQ)=vecr_(2)` such that `anglePOq=triangletheta Angular speed `= omega=triangletheta//triangle t " Let, "vecv_(1) and vecv_(2)` are the velocity vectors of the particle at P and Q respectively.
Since the speed is uniform, `|vecPA|=|vecQB|=v`
To find the change in the velocity in the given time interval, draw `overset(-)(P'A') and overset(-)(P'B')" as the velocity vectors "overset(-)v_(1) and overset(-)v_(2)`
From triangle law of vectors: `overset(-)P' A'+ overset(-)A'B'=overset(-)P'B or =overset(-)(A'B') =overset(-)(P'B')- overset(-)(P'A') =overset(-)(v_(2))-overset(-)(v_(1))=trianglevect`
As `triangle to 0 A'B'` would be arc of A'B' of circle of radius P'A' = v
`therefore triangletheta=A'B'//P'A' =|trianglev|//|vecv|, omegatrignalet=|trianglevecv|//|vecv| and |trianglevecv|//|trianglevect|= |vecv|omega=(omega r)omega=omega^(2) r [v=omegar]`
When `trianglet to 0" then " |trianglevecv|//|trianglevect|` would be magnitude of centripetal acceleration at P and given as, `|veca|=|trianglevecv|//|trianglet|=omega^(2)r=(v//r)^(2)r=v^(2)//r`
Thus, `|veca|=omega^(2)=v^(2)//r`
This given the magnitude of the acceleration of a particle in uniform circular motion.
Direction of acceleration: As `trianglet` tends to zero, the angle `triangletheta` also approaches zero. In this limit, as AB= AC, so `angleABC=angleACB=90^(@)`. Thus, the change in velocity `trianglevecv` and hence the acceleration `veca` is perpendicular to the velocity vector `vecv_(1) " But "vecv_(1)` is directed along tangent at point P, so acceleration `veca` act along the radius towards the centre of the circle. Such an acceleration is called centripetal acceleration.
Its magnitude remains constant `(=v^(2)/r)` but its direction continuously changes and remains perpendicular to the velocity vector at all positions.