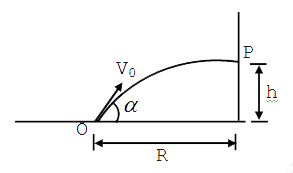
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A cannon on a level plane is aimed at an angle theta above the horizon...
Text Solution
|
- Two identical shells are fired from a point on the ground with same mu...
Text Solution
|
- Two identical shells are fired from a point on the ground with same mu...
Text Solution
|
- Two identical shells are fired from a point on the ground with same mu...
Text Solution
|
- Two identical shells are fired from a point on the ground with same mu...
Text Solution
|
- Shots are fired simultaneously from the top and the bottom of a vertic...
Text Solution
|
- A cannon of mass 5m (including a shell of mass m) is at rest on a smoo...
Text Solution
|
- A cannon on a level plane is aimed at an angle theta above the horizon...
Text Solution
|
- Shots are fired simu ltaneou ly from the top and bottom of a vertical ...
Text Solution
|