Home
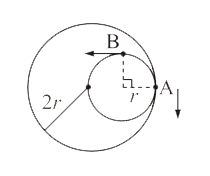
Class 12
PHYSICS
A and B are moving in two circular orbit...

A and B are moving in two circular orbits with angular velocity
`2 omega and omega` respectively. Their position are shown at t = 0. Find the time at which they will meet for 1st time

A

`pi/(2omega)`

B

`(3pi)/(2omega)`

C

`pi/(omega)`

D

They will never meet

Text Solution

Verified by Experts

The correct Answer is:
D
They can meet only at the initial position of A.
time after which A reach this position `=pi/(omega),(2pi)/(omega), (3pi)/(omega),....=(npi)/(omega)`
time after which B reach this position `=(3pi)/(2omega)+n (2pi)/(omega)`
They will never be able to meet as for no value of and these two terms will be same.
Promotional Banner

Similar Questions

Explore conceptually related problems

Two discs A and B are in contact and rotating with angular velocity with angular velocities omega_(1) and omega_(2) respectively as shown. If there is no slipping between the discs, then

Two particle 'A' and 'B' are moving on the same circle with angular omega_(1) and omega_(2) respectively w.r.t. the centre of circle. Find the angular velocity of 'A' w.r.t. 'B' when, (i) their sense of rotations is same, (ii) and their sense of rotation is opposite.

A particle moves in a circular path of radius R with an angualr velocity omega=a-bt , where a and b are positive constants and t is time. The magnitude of the acceleration of the particle after time (2a)/(b) is

Two particles A and B are moving in a horizontal plane anitclockwise on two different concentric circles with different constant angular velocities 2omega and omega respectively. Find the relative velocity (in m/s) of B w.r.t. A after tome t=pi//omega . They both start at the position as shown in figure ("Take" omega=3rad//sec, r=2m)

A conical pendulum is moving in a circle with angular velocity omega as shown. If tension in the string is T, which of following equations are correct ?

A partical excutes SHM with amplitude A and angular frequency omega . At an instant the partical is at a distance A//5 from the mean position and is moving away from it. Find the time after which it will come back t this position again and also find the time after which it will pass through the mean position.

A particle is moving in a circular orbit of radius r_(1) with an angular velocity omega_(1) It jumps to another circular orbit of radius r_(2) and attains an angular velocity omega_(2) . If r_(2)= 0.5 r_(1) , and if no external torque is applied to the system, then the new angular velocity omega_(2) is given by

If a particle goes round the circle once in a time period T, then the angular velocity omega will be

A satellite of mass m revolves around the earth of mass M in a circular orbit of radius r , with an angular velocity omega . If raduis of the orbit becomes 9r , then angular velocity of this orbit becomes