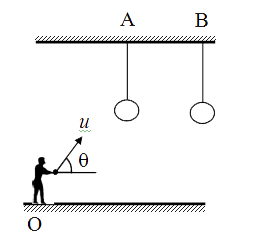
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two rings are suspended from the points A and B on the ceiling of a ro...
Text Solution
|
- Two small balls, each having equal positive charge Q are suspended by ...
Text Solution
|
- Two small balls A and B of mass M and 3M hang from the ceiling by stri...
Text Solution
|
- Two identical small bodies each of mass m and charge q are suspended ...
Text Solution
|
- Two rings are suspended from the points A and B on the ceiling of a ro...
Text Solution
|
- Two rings are suspended from the points A and B on the ceiling of a ro...
Text Solution
|
- Two rings are suspended from the points A and B on the ceiling of a ro...
Text Solution
|
- Two rings are suspended from the points A and B on the ceiling of a ro...
Text Solution
|
- Two rings are suspended from the points A and B on the ceiling of a ro...
Text Solution
|