Home
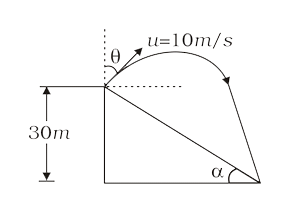
Class 12
PHYSICS
A ball is thrown upwards from the top of...

A ball is thrown upwards from the top of an incline with angle of projection `theta` with the vertical as shown. Take `theta = 60^(@)` and `g=10 m//s^(2)` . The ball lands exactly at the foot of the incline.

The time of flight of the ball is:

A

`t=sqrt(3) s`

B

t = 4 s

C

t = 3 s

D

t = 6 s

Text Solution

Verified by Experts

The correct Answer is:
C
`u_(y)=10 cos 60^(@) =5m//s rArr 5t-1/2 gt^(2)=-30 rArr t^(2)-t-6=0 rArr t=3s `
Promotional Banner

Similar Questions

Explore conceptually related problems

A ball is thrown upwards from the top of an incline with angle of projection theta with the vertical as shown. Take theta = 60^(@) and g=10 m//s^(2) . The ball lands exactly at the foot of the incline. The angle of inclination of incline alpha is:

A ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.

A ball is thrown upwards from the top of a tower 40 m high with a velocity of 10 m//s. Find the time when it strikes the ground. Take g=10 m//s^2 .

A ball is thrown upwards from the ground with an initial speed of u. The ball is at height of 80m at two times, the time interval being 6 s. Find u. Take g=10 m//s^2.

A ball is thrown vertically upwards from the ground. Work done by air resistance during its time of flight is

A ball is thrown upward with speed 10 m/s from the top to the tower reaches the ground with a speed 20 m/s. The height of the tower is [Take g=10m//s^(2) ]

A ball is projected from the bottom of an inclined plane of inclination 30^@ , with a velocity of 30 ms^(-1) , at an angle of 30^@ with the inclined plane. If g = 10 ms^(-2) , then the range of the ball on given inclined plane is

A ball is thrown downwards with a speed of 20 ms^(–1) from top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30 ms^(–1) from the foot of the building. Find the time after which both the balls will meet - (g = 10 ms^(–2))

Two balls are thrown from an inclined plane at angle of projection alpha with the plane, one up the incline and other down the incline as shown in figure ( T stands for total time of flight):