A
B
C
D
Text Solution
Verified by Experts
Recommended Questions
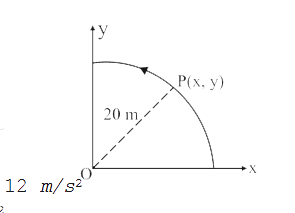
- A point P moves in counter-clockwise direction on a circular path as s...
Text Solution
|
- A point p moves in counter - clockwise direction on a circular path as...
Text Solution
|
- A point P moves in counter clockwise direction on a circular path as s...
Text Solution
|
- A point P moves in counter-clockwise direction on figure. The movement...
Text Solution
|
- एक बिंदु P व्रतकार पथ पर वामावर्त दिशा में चलता है जैसा की चित्र में द...
Text Solution
|
- A point P moves in a counter-clockwise direction on a circular path as...
Text Solution
|
- A point P moves in counter-clockwise direction on a circular path as s...
Text Solution
|
- एक बिंदु P एक वृत्तीयपथ पर वामवर्ती दिशा में गतिमान है | P की गति इस प...
Text Solution
|
- एक बिंदुP एक वृत्तीय पथ पर वामावर्त दिशा में गतिशील है जैसा की चित्र ...
Text Solution
|