Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
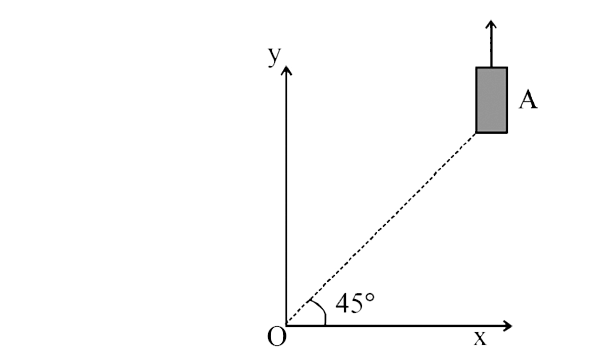
- On a frictionless horizontal surface , assumed to be the x-y plane ,...
Text Solution
|
- The eccentricity of the ellipse which meets the straight line (x)/(7)+...
Text Solution
|
- On a frictionless horizontal surface , assumed to be the x-y plane , a...
Text Solution
|
- A small cart A starts moving on a horizontal surface, assumed to be x-...
Text Solution
|
- A gun is mounted on a trolley which can move uniformly with speed v m/...
Text Solution
|
- An electron is moving with constant velocity along x-axis. If a unifor...
Text Solution
|
- वक्रों पर बिंदु ( बिंदुओं ) को निकालें : y=x^2, जहां स्पर्श रेखा x...
Text Solution
|
- एक चोटी ट्रॉली A किसी घर्षणरहित क्षैतिज पृष्ट पर (माना xy तल में ) (sq...
Text Solution
|
- துகள் ஒன்று மாறாத திசைவேகத்துடன் X அச்சுக்கு இணையான நேர்கோட்டின் வழியே...
Text Solution
|