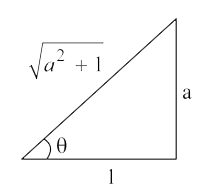
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- STATEMENT -1 : For an observer looking out through the window of a fa...
Text Solution
|
- STATEMENT -1 : For an observer looking out through the window of a fas...
Text Solution
|
- Explain this common observation clearly : If you look out of the windo...
Text Solution
|
- वस्तु A का वेग v(A) है तथा वस्तु B का वेग v(B) है दोनों एक रेखा में ए...
Text Solution
|
- A car is moving with velocity vec v(c) towards north and a train is mo...
Text Solution
|
- कथन I एक तीव्रगामी रेलगाड़ी की खिड़की से बाहर देखते प्रेक्षक को निकट की ...
Text Solution
|
- When an observer is standing on earth, the trees and houses appear sta...
Text Solution
|
- When an observer is standing on earth, the trees and houses appear sta...
Text Solution
|
- Explain this common observation clearly: If you look out of the window...
Text Solution
|