Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
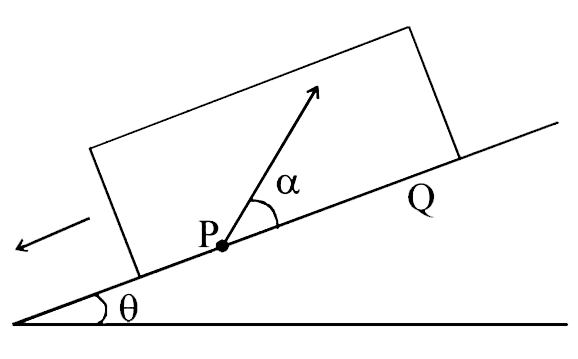
- A large , heavy box is sliding without friction down a smooth plane o...
Text Solution
|
- A large , heavy box is sliding without friction down a smooth plane o...
Text Solution
|
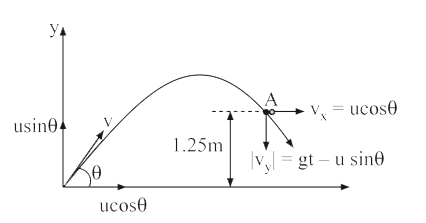
- A box is falling freely. Inside the box, a particle is projected with ...
Text Solution
|
- A box is failing freely. Inside the box, a particle is projected with ...
Text Solution
|
- A very heavy box is kept on a frictionless incline plane inclined at a...
Text Solution
|
- A large box is moving on a horizontal floor with constant acceleration...
Text Solution
|
- A rectangular box lies on a rough inclined surface. The coefficient of...
Text Solution
|
- A box is lying on an inclined plane if the box slides when the angle o...
Text Solution
|
- A wooden box is lying on an inclined plane. What is the coefficient of...
Text Solution
|