Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
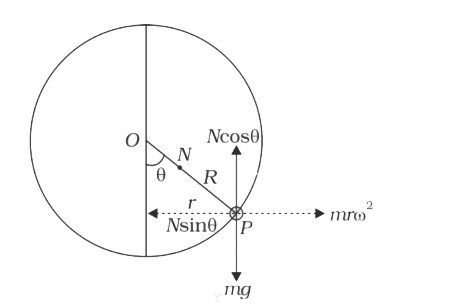
- A thin circular wire of radius R rotatites about its vertical diameter...
Text Solution
|
- A thin circular wire of radius R rotatites about its vertical diameter...
Text Solution
|
- A thin ring of radius R is made of a material of density rho and Young...
Text Solution
|
- A smooth wire is bent into a vertical circle of radius a. A bead P can...
Text Solution
|
- A small bead of mass 'm' is threaded on a frictionless circulat wire o...
Text Solution
|
- A circular wire frame of radius R is rotating about its fixed vertical...
Text Solution
|
- R त्रिज्या का पतला वृत्तीय तार अपने ऊर्ध्वाधर व्यास के परितः कोणीय आवृ...
Text Solution
|
- A thin circular loop of radius R rotates about its vertical diameter w...
Text Solution
|
- A circular loop has a small bead which can slide on it without frictio...
Text Solution
|