A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The block of mass m is at rest. Find the tension in the string A .
Text Solution
|
- The block shown in figure has a mass M and descends with an accelerati...
Text Solution
|
- Two blocks o equal mass m are tied to each other through light string...
Text Solution
|
- A block of mass 30 kg is suspended by three string as shown in fig, Fi...
Text Solution
|
- A block of mass M si suspended by two strings angles theta(1) and thet...
Text Solution
|
- Figure-2.64 shows a block of mass M supporting a bar of mass m through...
Text Solution
|
- A block of mass 2 kg is kept at rest on a smooth inclied plane as show...
Text Solution
|
- Two blocks of masses m and M are connected by an inextensible light st...
Text Solution
|
- The block of mass m is at rest. Find the tension in the string A .
Text Solution
|
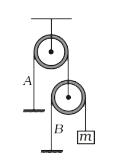
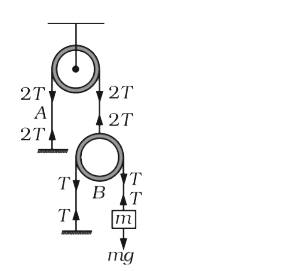 so, tenison in string A is 2 mg
so, tenison in string A is 2 mg