A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A block of mass m is pressed against a wall by a spring as shown in th...
Text Solution
|
- A block of mass m is attached to one end of a mass less spring of spri...
Text Solution
|
- A block pressed against the vertical wall is in equilibrium. The minim...
Text Solution
|
- A block of mass m is moving with a speed v on a horizontal rough surfa...
Text Solution
|
- In the figure shown, a spring of spring constant K is fixed at on end ...
Text Solution
|
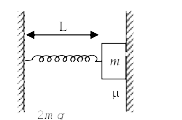
- Block of mass 2 m is given v(0) towards the right. If L is the natural...
Text Solution
|
- Two springs are in a series combination and are attached to a block of...
Text Solution
|
- A system consists of block A and B each of mass m connected by a light...
Text Solution
|
- A block of mass m compresses a spring iof stifffness k through a dista...
Text Solution
|