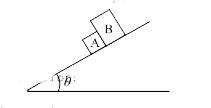
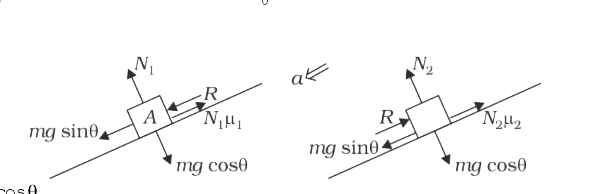A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The two blocks A and B of equal mass are initially in contact when rel...
Text Solution
|
- Consider the situation shown in figure in which a book 'A' of mass 2 k...
Text Solution
|
- Consider the situation shown in figure in which a book 'A' of mass 2 k...
Text Solution
|
- Consider the situation shown in figure in which a book 'A' of mass 2 k...
Text Solution
|
- Two blocks are in contect moving on an inclined plane of inclination a...
Text Solution
|
- Consider the situation as shown in the figure. If mu(1) is the frictio...
Text Solution
|
- Two blocks are kept on an inclined plane and tied to each other with a...
Text Solution
|
- The coefficient of friction between the block A of mass m & block B of...
Text Solution
|
- consider the situation shown in figure in which a block 'A' of mass 2 ...
Text Solution
|