Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The inclined surface is rough mu = (1)/(2). For different values of m ...
Text Solution
|
- Let M be the maximum and m be the minimum value of |2/(3+i e^(itheta))...
Text Solution
|
- If the coefficient of friction between M and the inclined surfaces is ...
Text Solution
|
- The inclined surface is rough mu = (1)/(2) . For different values of m...
Text Solution
|
- Block M slides down on frictionless incline as shown. The minimum fric...
Text Solution
|
- यदि m+1/(m-2)=4 है तो (m-2)^(2)+1/((m-2)^(2)) का मान ज्ञात करें?
Text Solution
|
- A body of mass m slides down a rough plane of inclination alpha . If m...
Text Solution
|
- There is an inclined plane with length 13 m, heght 5 m and mu = (1)/(3...
Text Solution
|
- A body of mass m slides down a rough plane of inclination alpha . If m...
Text Solution
|
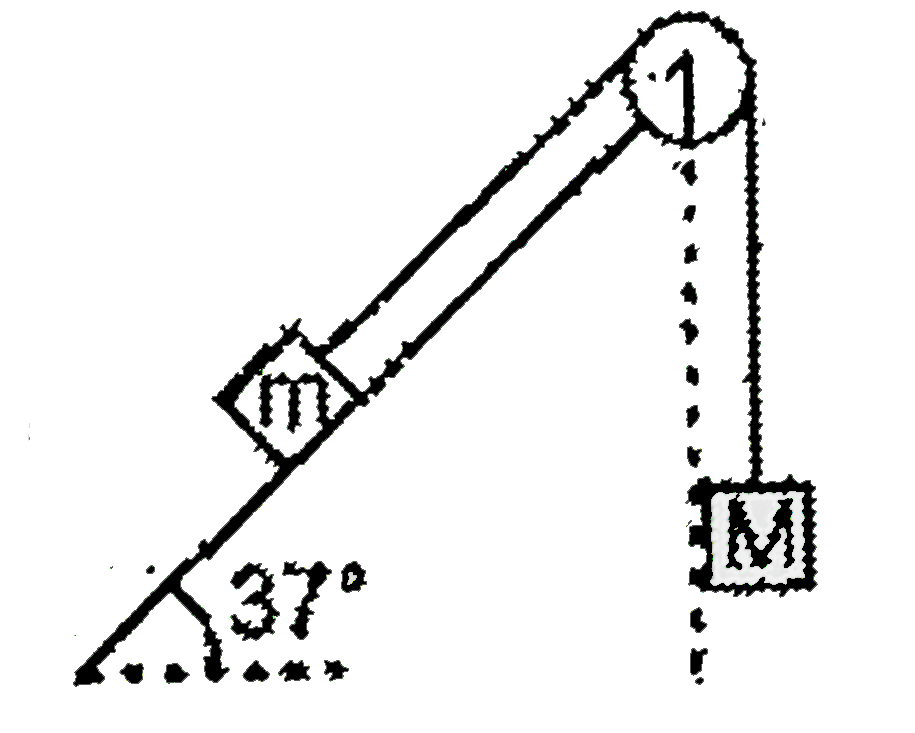
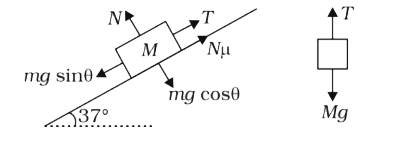 `implies T = mg`
`implies T = mg` 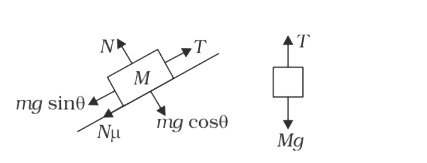 `implies M = m (sin theta + mu cos theta)`
`implies M = m (sin theta + mu cos theta)` 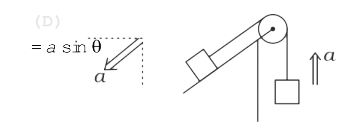 And vertical acc of M = a
And vertical acc of M = a