Home
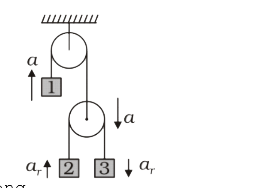
Class 12
PHYSICS
In the figure shown,a(3) = 6 m//s^(2) (d...

In the figure shown,`a_(3) = 6 m//s^(2)` (downwards) and `a_(2) = 4 m//s^(2)` (upwards) .Find acceleration of `1`

A

`1m//s^(2)` downwards

B

`2 m//s^(2)` upwards

C

`1 m//s^(2)` upwards

D

`2m//s^(2)` downwards

Text Solution

Verified by Experts

The correct Answer is:
C
`a_(3) = a + a_(r ) = 6`
`a_(2) = a_(r ) - a = 4`
On solving these two equations, we get `a = 1m//s^(2)`
Promotional Banner

Similar Questions

Explore conceptually related problems

In the figure shown, a_(3) = 6 m//s^(2) (downwards) and a_(3) = 6 m//s^(2) (upwards) .Find acceleration of 1

In the figure acceleration of A is 1m//s^(2) upward, acceleration of B is 7m//s^(2) upward acceleration of C is 2m//s^(2) upward. The acceleration of D will be.

A block of mass 2 kg is placed on a truck as shown in the figure. The coefficient of friction between the block and surface is 0.5 . The truck starts from the rest and moves with acceleration a_(0) . (a) Find the friction force acting on the block if (i) a_(0) = 2 m//s^(2) , (ii) 4 m//s^(2) , (iii) 6 m//s^(2) and (b) if acceleration of truck a_(0) = 8 m//s^(2) . After how much time the blocks falls off the truck and the distance travelled by the truck in this time.

If acceleration of block B is 4 m//s^(2) upward & that of C is 6 m//s^(2) downward. Find acceleration of A :-

In the adjoining figure velocities and acceleration of the blocks 1 and 3 at any instant are v_(1) = 6 m//s upwards , a_(1) = 6 m//s^(2) ( downwards ) and v_(3) = 3m//s ( upwards) ,a_(3) = 4 m/s^(2) ( downward) respectively. Find the velocity and the acceleration of the block 2 at that instant.

In the figure shown, the acceleration of block of mass m_(2) is 2m//s^(2) . The acceleration of m_(1) :

A mass m of volume V=10cm^(2) is tied with a string to the base of a container filled with a liquid of density (P_(l)=10^(3)kg//m^(3)) as shown in the figure. The container is then accelerated with acceleration (a_(x)=9m//s^(2)) and (a_(y)=2m//s^(2)) a shown in the figure. [ g=10((m)/(s^(2))) acceleration due to gravity] the net buoyancy force acting on the mass is

In each case m_(1) = 4 kg and m_(2) = 3 kg . If a_(1) and a_(2) and a_(3) are the respective acceleration of the block m_(1) in given situation, then

In the figure shown, acceleration of 1 is x (upwards). Acceleration of pulley P_(3) , w.r.t. pulley P_(2) is y (downwards) and acceleration of 4 w.r.t. to pulley P_(3) is z (upwards). Taking upward +ve and downward -ve then {:(,"Column I",,,"Column II"),((A),"Absolute acceleration of 2",,(p),(y-x) "downwards"),((B),"Absolute acceleration of 3",,(q),(z-x-y) "upwards"),((C),"Absolute acceleration of 4",,(r),(x+y+z) "downwards"),(,,,(s),"None"):}