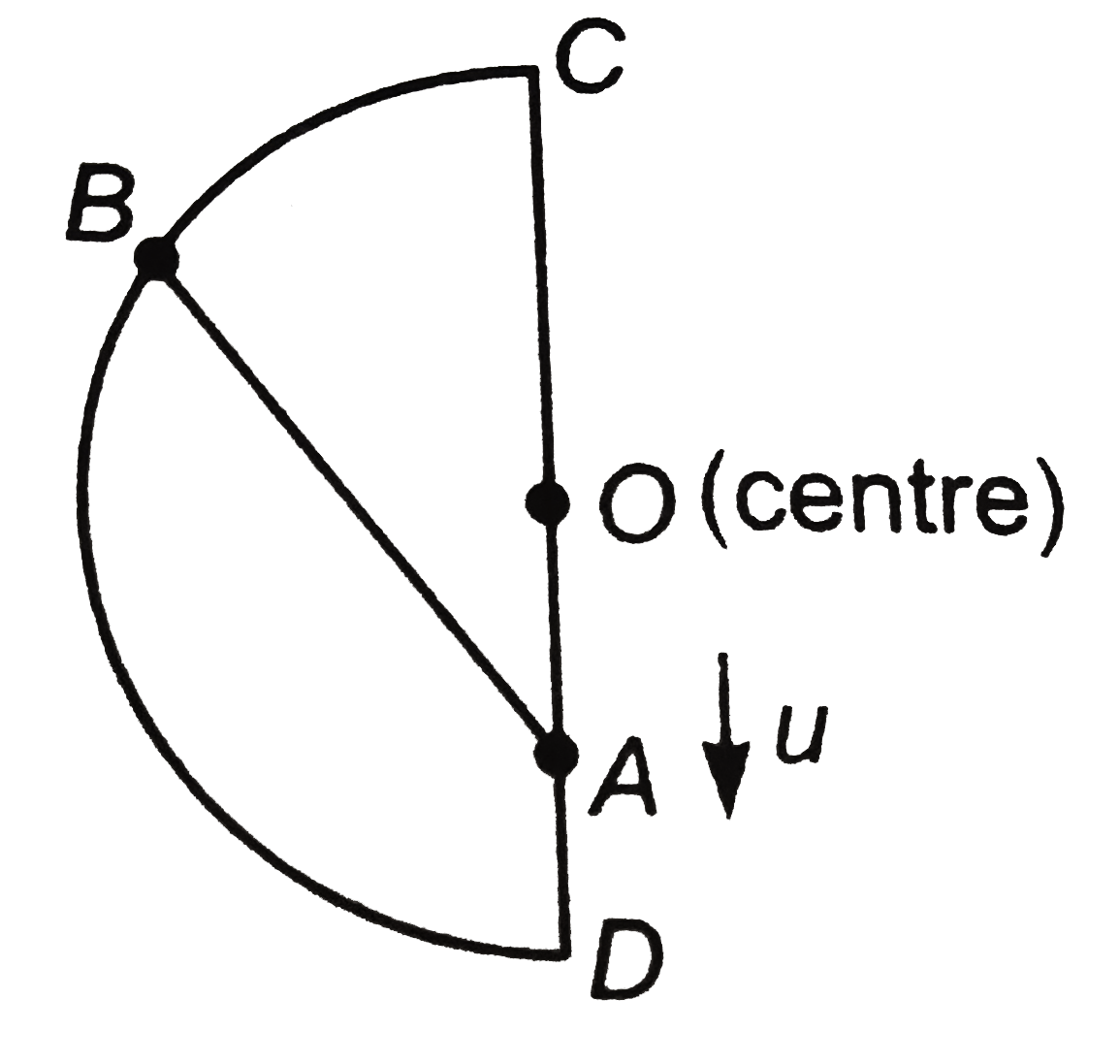
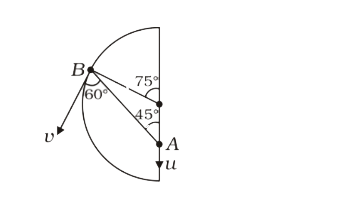
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two beads A and B move along a semicircular wire frame as shown in fig...
Text Solution
|
- A wire, which passes through the hole in a small bead, is bent in the ...
Text Solution
|
- Two block A and Bmove along a semicircular wire frame as shown in figu...
Text Solution
|
- A U -shaped wire has a semicircular bending between A and B as shown i...
Text Solution
|
- A bead of mass m is threaded on a smooth circular wire centre O, radiu...
Text Solution
|
- A bead of mass m is threaded on a smooth circular wire centre O, radiu...
Text Solution
|
- A bead of mass m is threaded on a smooth circular wire centre O, radiu...
Text Solution
|
- A semicircular wire frame of radius R is standing vertical on a horizo...
Text Solution
|
- A fixed U-shaped smooth wire has a semi-circular bending between A and...
Text Solution
|