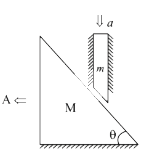
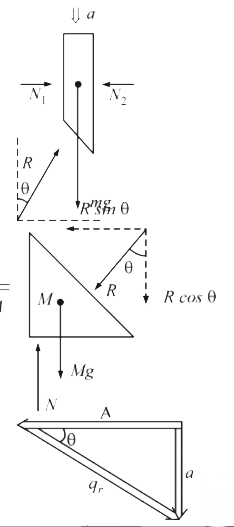
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A block of mass m placed on the inclined surface of wedge of mass M. B...
Text Solution
|
- A small block of mass m is placed at rest on the top of a smooth wedge...
Text Solution
|
- A block of mass m is placed at rest on a smooth wedge of mass M placed...
Text Solution
|
- A block of mass m is placed on the inclined sufrace of a wedge as show...
Text Solution
|
- In fig. mass m is being pulled on the incline of a wedge of mass M. Al...
Text Solution
|
- A block of mass m is placed on a smooth wedge of inclination. The whol...
Text Solution
|
- Block A of mass m is placed over a wedge of same mass m. Both the bloc...
Text Solution
|
- In the Fig. shown, mass 'm' is being pulled on the incline of a wedge ...
Text Solution
|
- A block of mass m placed on the inclined surface of wedge of mass M. B...
Text Solution
|