Home
Class 12
PHYSICS
From the fixed pulley, masses 2 kg, 1 kg...

From the fixed pulley, masses 2 kg, 1 kg and 3 kg are suspended as shown is figure. Find the extension in the spring when acceleration of 3 kg and 1 kg is same if spring constant of the spring k = 100 N/m. (Take `g = 10 ms^(-2)`)

A

10 cm

B

20 cm

C

30 cm

D

25 cm

Text Solution

Verified by Experts

The correct Answer is:
B
T - 20 = 20….(i) 10 + kx - T = a …(2) 30 - kx = 3a …..(3)
Adding all the equation 10 + 30 - 20 a `implies (10)/(3) m//s^(2)`
`implies x = (30 - 3a)/(k) = (30 - 3 xx (10)/(3))/(100) = (20)/(100) n`
Promotional Banner

Similar Questions

Explore conceptually related problems

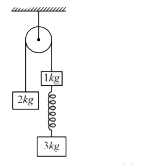
From the fixed pulley, masses 2kg, 1kg and 3kg are suspended as shown in the figure. Find the extension in the spring if k=100 N//m . (Neglect oscillations due to spring)

Two block of mass 4 kg and 5 kg attached a light spring are suspended by a string as shown in figure. Find acceleration of block 5 kg and 4 kg just after the string is cut.

Find the acceleration of 3 kg mass when acceleration of 2 kg mass is 2ms^(-2) as shown in figure-2.140

As shown in the figure, two equal masses each of 2kg are suspended from a spring balance. The reading of the spring balance will be.

Consider three cases, same spring is attached with 2kg , 3kg and 1kg blocks as shown in figure. If x_(1) , x_(2) , x_(3) be the extensions in the spring in the three cases, then.

The time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is

Two blocks of masses 1 kg and 3 kg are moving with velocities 2 m//s and 1 m//s , respectively , as shown. If the spring constant is 75 N//m , the maximum compression of the spring is

System shown in figure is released from rest . Pulley and spring is massless and friction is absent everywhere. The speed of 5 kg block when 2 kg block leaves the contact with ground is (force constant of spring k = 40 N//m and g = 10 m//s^(2))

Force constant of a spring is 100 N//m . If a 10kg block attached with the spring is at rest, then find extension in the spring. ( g= 10 m//s^(2) )