Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
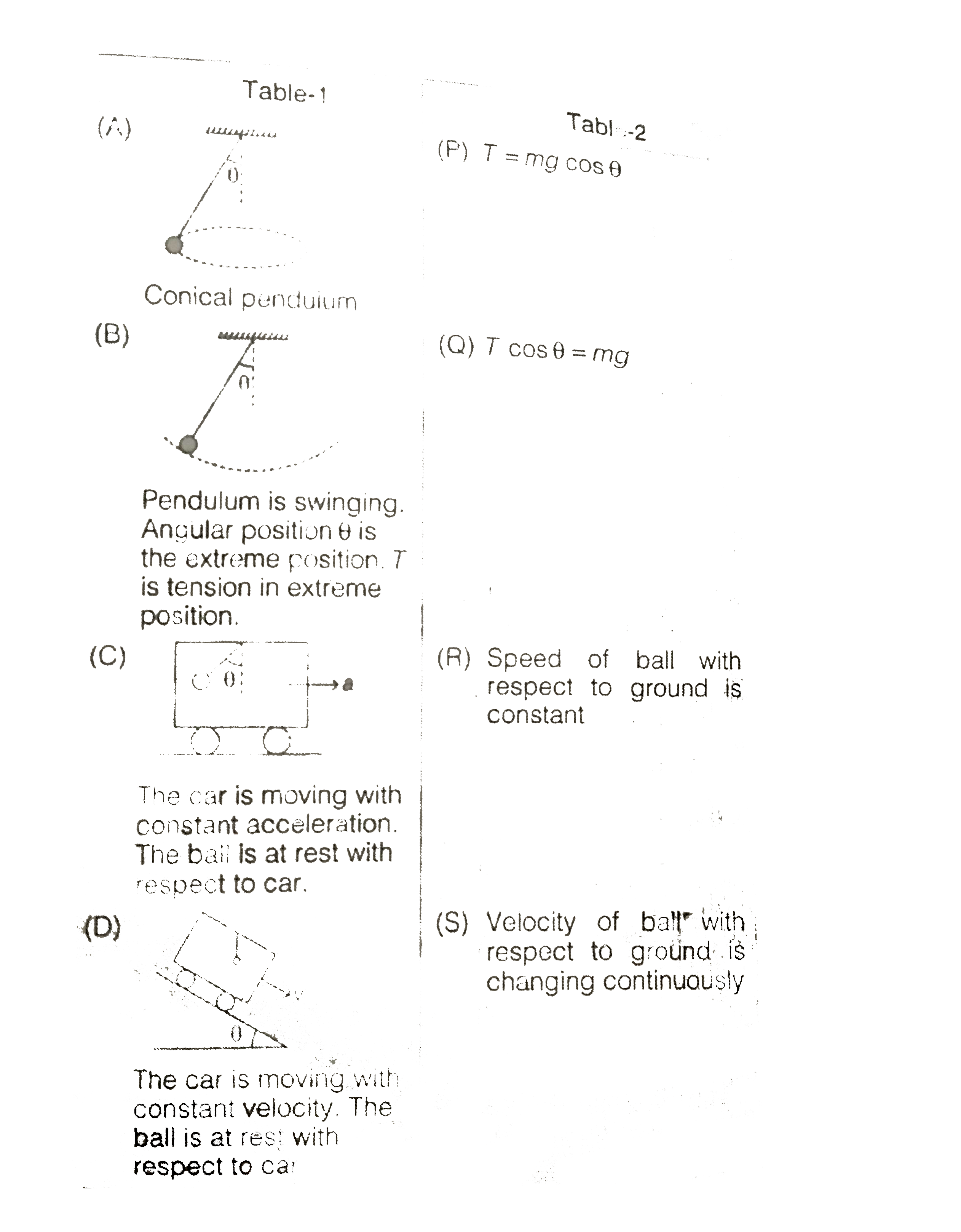
- In all the four situations depicted in Table-1, a ball of mass m is co...
Text Solution
|
- A small ball of mass m is connected by an inextensible massless string...
Text Solution
|
- A simple pendulum consists of a ball of mass m connected to a string o...
Text Solution
|
- Find tension /tensions in the string/strings in the following cases:
Text Solution
|
- A 2 kg block is lying on a smooth table which is connected by a body o...
Text Solution
|
- In column-1 a situation is depicted each of which is in vertical plane...
Text Solution
|
- In all the four situations depicted in Table-1, a ball of mass m is co...
Text Solution
|
- Four point size metal spheres each of mass 1 kg are placed on a turn t...
Text Solution
|
- किसी घर्षणरहित मेज पर रखे 10 किग्रा तथा 20 किग्रा के दो पिण्ड किसी पतल...
Text Solution
|