Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
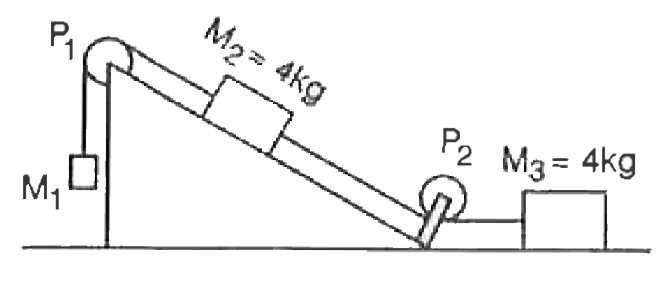
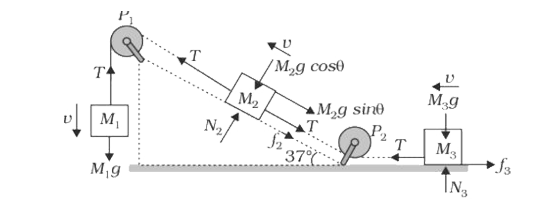
- Masses M(1),M(2) and M(3) are connected by string of negligible mass w...
Text Solution
|
- The block each of mass 1 kg are placed as shown .They are connected by...
Text Solution
|
- A system consists of three masses m(1) , m(1) , m(1) , m(2) and m(3) c...
Text Solution
|
- Three blocks of masses m(1), m(2) and M are arranged as shown in figur...
Text Solution
|
- Blocks of mass M(1) and M(2) are connected by a cord which passes over...
Text Solution
|
- Masses M(1),M(2) and M(3) are connected by string of negligible mass w...
Text Solution
|
- Two masses m(1) kg and m(2) kg passes over an atwoods machine. Find th...
Text Solution
|
- A system consists of three masses m(1),m(2) " and " m(3) connected by ...
Text Solution
|
- Two masses m(1) and m(2) ( m(2) gt m(1)) are hanging vertically over f...
Text Solution
|