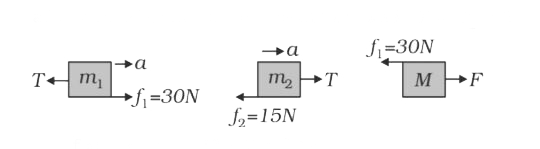Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
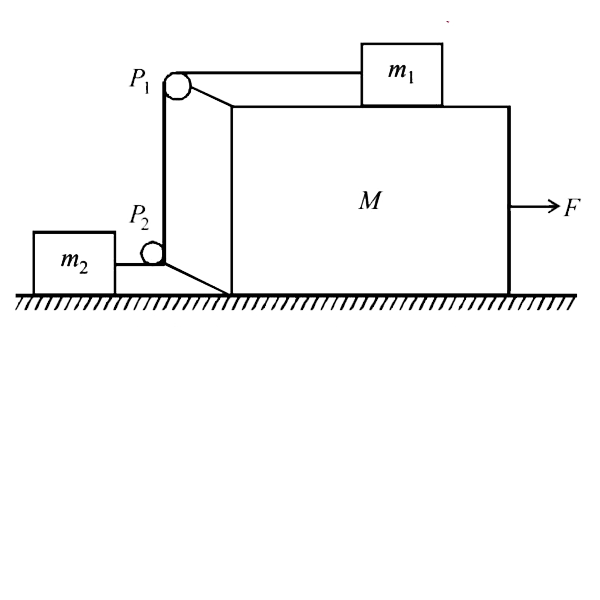
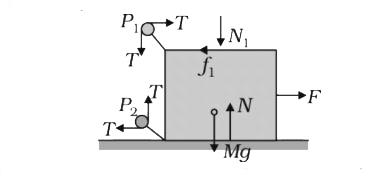
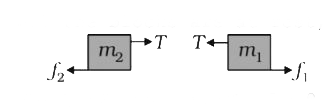
- In the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively...
Text Solution
|
- Masses M1 , M2 and M3 are connected by strings of negligible mass whic...
Text Solution
|
- In the figure , masses m(1) , m(2) and M are 20 kg , 5 kg and 50 kg re...
Text Solution
|
- Three blocks are arranged on a horizontal table ABCD as shown in the f...
Text Solution
|
- A mass 'M' is broken into two parts of masses m1" and "m2 . How are m1...
Text Solution
|
- A mass M is broken into two parts of masses m1 and m2 . How are m1 and...
Text Solution
|
- If two masses m1 and m2 (m1 gt m2) tied to string moving over a fricti...
Text Solution
|
- Three masses m1 = m ,m2 = 2m and m3 = 3m are hund on a string passing ...
Text Solution
|
- Gravitational force between masses m1 and m2 is F. If a third mass m3 ...
Text Solution
|