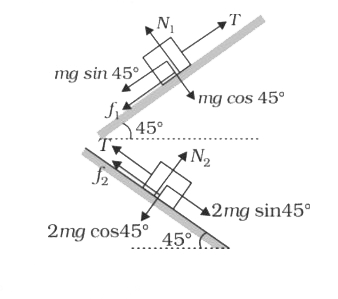Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
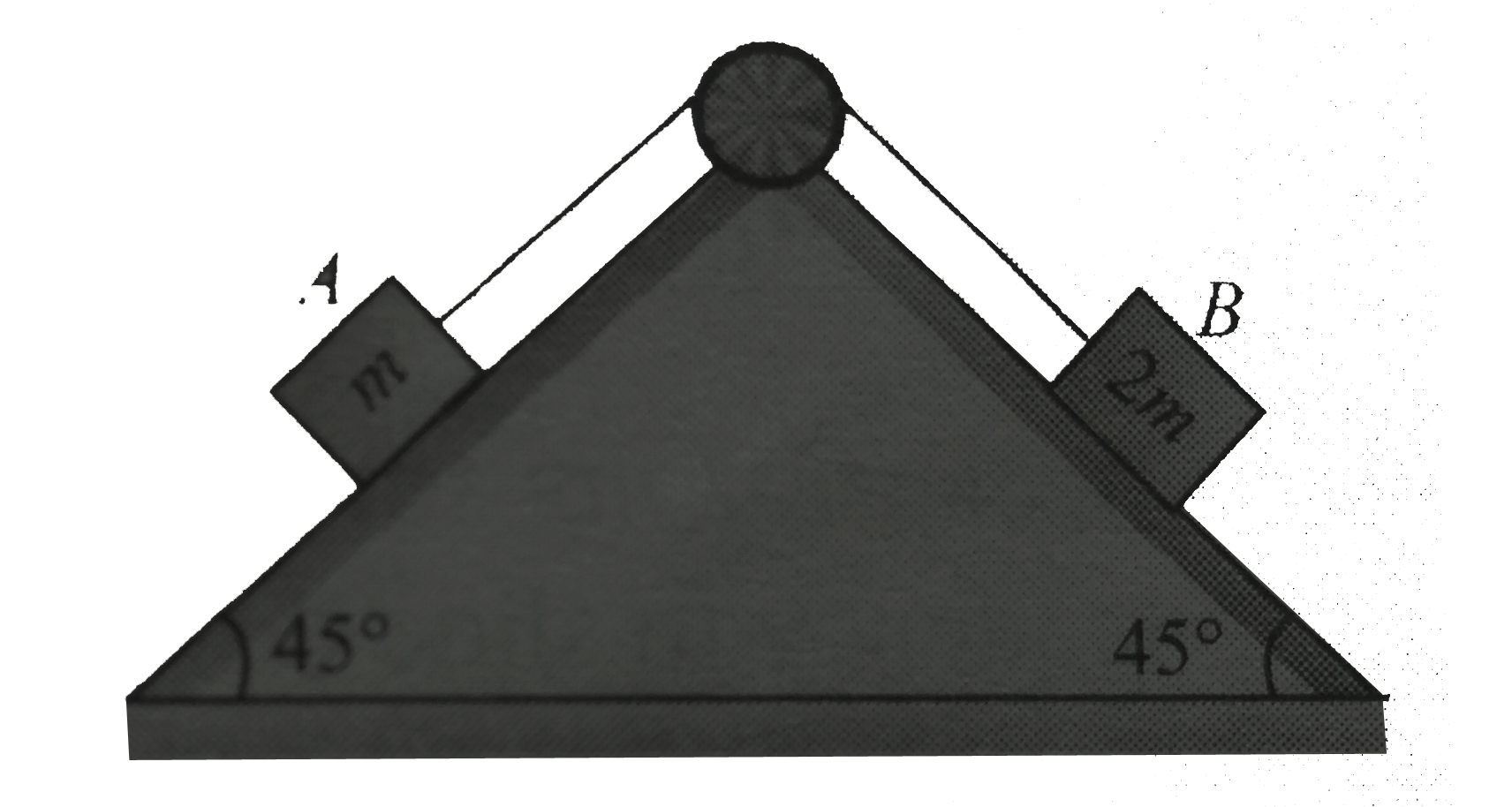
- Block A of mass m and block B of mass 2m are placed on a fixed triangu...
Text Solution
|
- A block of mass m is placed on the inclined sufrace of a wedge as show...
Text Solution
|
- Block A of mass m and block B of mass 2m are placed on a fixed triangu...
Text Solution
|
- The coefficient of friction between the block A of mass m and the tria...
Text Solution
|
- Block A of mass m and block B of mass 2m are placed on a fixed traingu...
Text Solution
|
- Block A of mass m and block B of mass 2m are placed on a fixed traingu...
Text Solution
|
- Block A of mass m and block B of mass 2m are placed on a fixed traingu...
Text Solution
|
- a Block of mass m is placed on a wedge of mass M there is no friction ...
Text Solution
|
- Block A of mass m and block B of mass 2m are placed on a fixed traingu...
Text Solution
|