Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
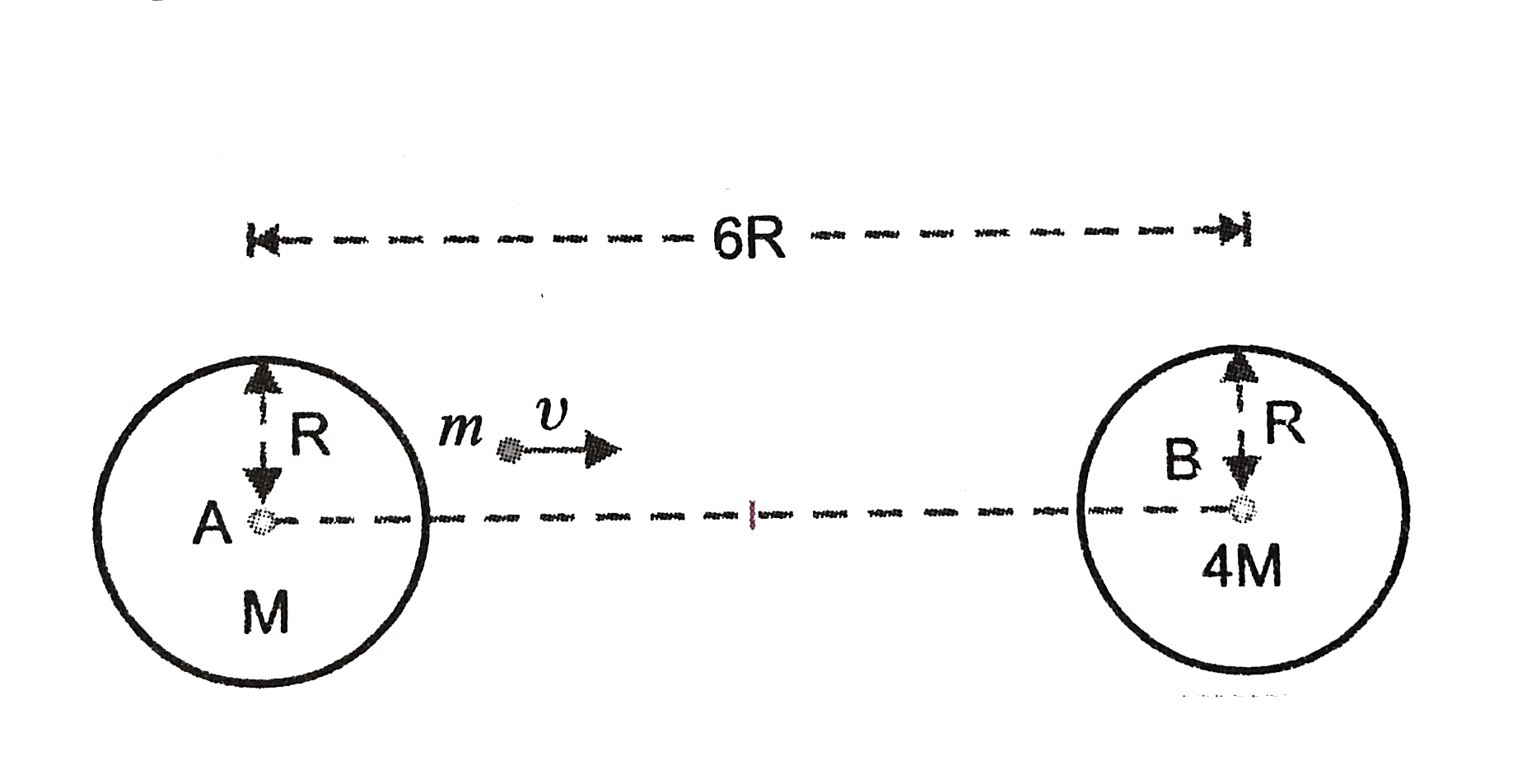
- Two uniform soild spheres of equal radii R but mass M and 4M have a ce...
Text Solution
|
- Two uniform soild spheres of equal radii R but mass M and 4M have a ce...
Text Solution
|
- Two solid spherical planets of equal radii R having masses 4M and 9M t...
Text Solution
|
- समान त्रिज्या R परन्तु M तथा 4M द्रव्यमान के दो एकसमान ठोस गोले इस प्र...
Text Solution
|
- समान त्रिज्या R परन्तु द्रव्यमान M तथा 4M द्रव्यमान के दो एकसमान ठोस ग...
Text Solution
|
- Two stars of masses M and 4M have radii x and 3x respectively. The dis...
Text Solution
|
- Two uniform solid spheres of equal radii R, but mass M and 4 M have a ...
Text Solution
|
- Two uniform solid spheres of equal radii R, but mass M and 4 M have a ...
Text Solution
|
- Two uniform solid spheres of equal radii R, but mass M and 4M have a c...
Text Solution
|