Home
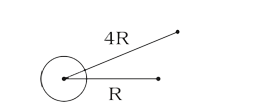
Class 12
PHYSICS
The ratio of distance of two satellites ...

The ratio of distance of two satellites from the centre of earth is `1:4`. The ratio of their time periods of rotation will be

A

`1:4`

B

`4:1`

C

`1:8`

D

`8:1`

Text Solution

Verified by Experts

The correct Answer is:
C
`(GMm)/R^2=(Mv^2)/R`
`v=sqrt((GM)/R) , T=(2piRsqrtR)/sqrt(GM)`
`T^2 oo R^3 , T_1/T_2=sqrt((1/4)^3)=1/4xx1/2=1/8`
Promotional Banner

Similar Questions

Explore conceptually related problems

The distance of two satellites from the surface of the earth R and 7R . There time periods of rotation are in the ratio

Then ratio of orbital radii of two satellites of a planet is 1:2 . what is the ratio of their time period?

The ratio of the distances of two planets from the sun is 1.38. The ratio of their period of revolution around the sun is

Two satellites A and B of the same mass are revolving around the earth in the concentric circular orbits such that the distance of satellite B from the centre of the earth is thrice as compared to the distance of the satellite A from the centre of the earth. The ratio of the centripetal force acting on B as compared to that on A is

Two satellites are at distances of 2R and 4R respectively from the surface of earth. The ratio of their time periods will be :

The distance of geostationary satellite from the centre of the earth (radius R) is nearest to

Two satellites of identical masses orbit the Earth at different heights. The ratio of their distance from the centre of earth is d : 1 and the ratio of the acceleration due to gravity at those heights is g : 1. Then the ratio of their orbital velocities is ________ .

Two small satellites are moving in circular orbits around the earth at a distance R and R + Delta R from the centre of the earth. If their time period of rotation are T and T + Delta T respectively, then