Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
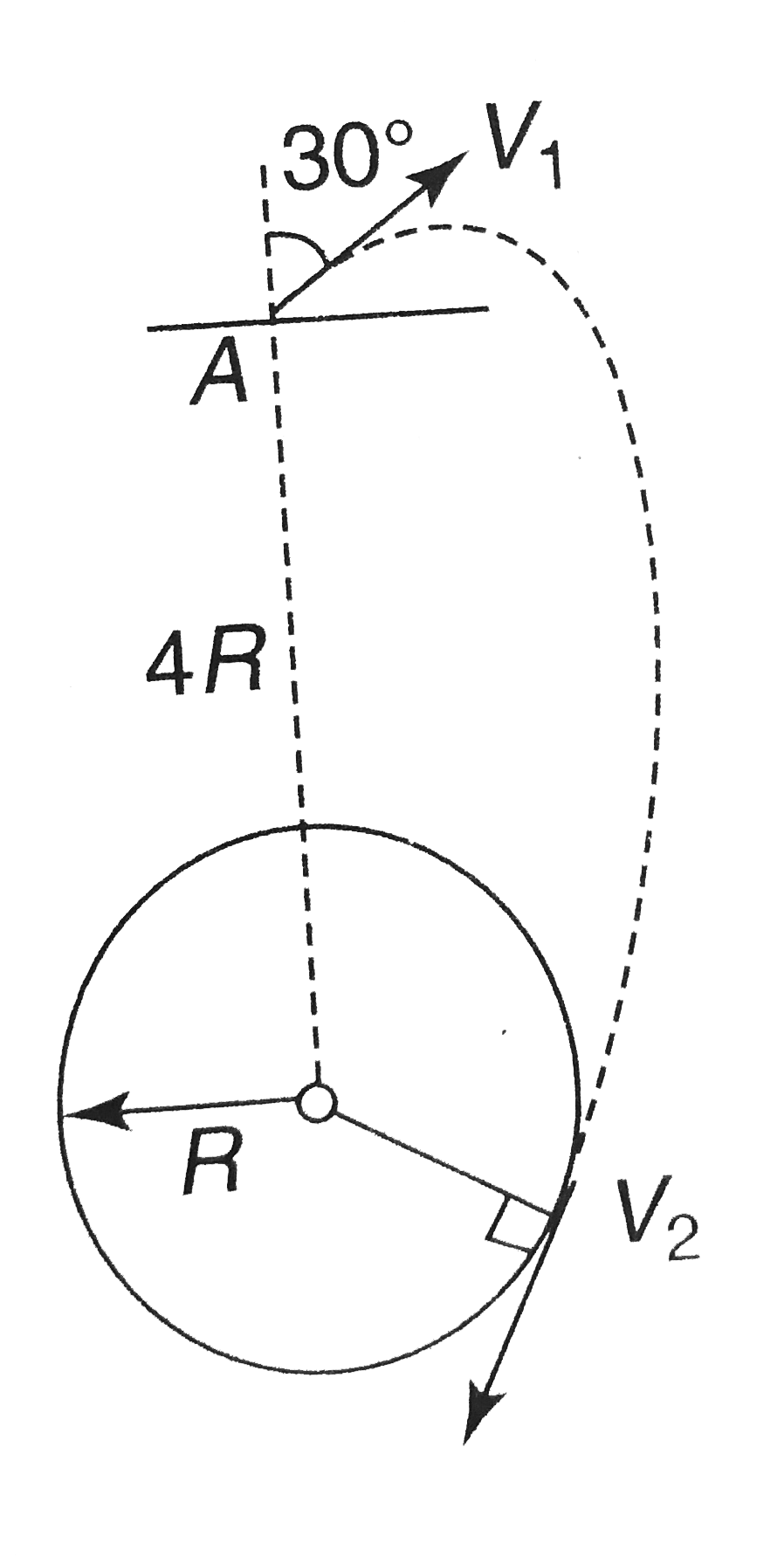
- A particle is projected from point A, that is at a distance 4R form th...
Text Solution
|
- A particle is projected from point A , that is at a distance 4R form t...
Text Solution
|
- Two particles of equal mass 'm' are projected from the ground with spe...
Text Solution
|
- A particle of mass m is projected from the surface of earth with a spe...
Text Solution
|
- A body at rest starts from a point at a distance r (gtR) from the cent...
Text Solution
|
- A particle is projected from the surface of the earth with a speed of ...
Text Solution
|
- A particle is projected from the surface of the earth with a speed of ...
Text Solution
|
- The minimum and maximum distance of a satellite from the centre of the...
Text Solution
|
- The minimum and maximum distance of a satellite from the centre of the...
Text Solution
|