Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
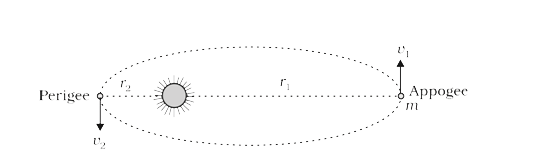
- A planet of mass m moves along an ellipse around the Sun so that its m...
Text Solution
|
- A planet of mass m revolves in elliptical orbit around the sun of mass...
Text Solution
|
- A planet of mass m moves along an ellipse around the Sun so that its m...
Text Solution
|
- A planet of mass m moves along an ellipse around the sun so that its m...
Text Solution
|
- A planet of mass m moves along an ellipse around the sum of mass M so ...
Text Solution
|
- A planet of mass m is moving in an elliptical orbit about the sun (mas...
Text Solution
|
- A planet of mass m moves in a elliptical orbit around an unknown...
Text Solution
|
- A planet of mass 'm' moves in an elliptical orbit around an unknown st...
Text Solution
|
- m द्रव्यमान का ग्रह सूर्य के चारों ओर दीर्घ वृत्ताकार कक्षा में गति कर...
Text Solution
|