Home
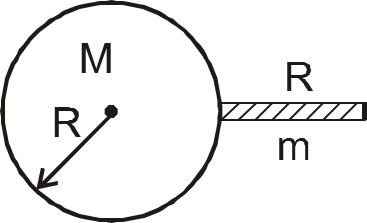
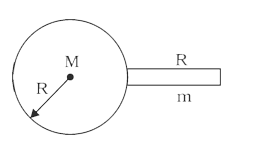
Class 12
PHYSICS
A uniform thin rod of mass m and length ...

A uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. If the magnitude of gravitational force exerted by earth on the rod is `(etaGMm)/(12R^(2))` then `eta` is

A

`(GmM)/(4R^2)`

B

`(GmM)/(2R^2)`

C

`(4GMm)/(9R^2)`

D

`(GMm)/(8R^2)`

Text Solution

Verified by Experts

The correct Answer is:
B
`dm=(mdx)/R , dF=(GM dm)/x^2 = (GM mdx)/(Rx^2)`
`F=int_R^(2R)(GMmdx)/(Rx^2)=(GMm)/R[-1/x]_R^(2R)=(GMm)/R[-(1/(2R) 1/R)]=(GMm)/(2R^2)`
Promotional Banner

Similar Questions

Explore conceptually related problems

A uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R . Then the magnitude of gravitational force exerted by earth on the rod is

If M is the mass of the earth and R its radius, then ratio of the gravitational acceleration and the gravitational constant is

If M is the mass of the earth and R its radius, the radio of the gravitational acceleration and the gravitational constant is

Work done in taking a body of mass m to a height nR above surface of earth will be : (R = radius of earth)

Gravitational potential energy of body of mass m at a height of h above the surface of earth (M = mass of earth , R = radius of earth) is

A small mass and a thin uniform rod each of mass 'm' are positioned along the same straight line as shown. Find the force of gravitational attraction exerted by the rod on the small mass.

A satellite of mass m is orbiting around the earth at a height h above the surface of the earth. Mass of the earth is M and its radius is R . The angular momentum of the satellite is independent of

A satellite of mass m is orbiting around the earth at a height h above the surface of the earth. Mass of the earth is M and its radius is R . The angular momentum of the satellite is independent of :

A body of mass m is placed on the earth's surface . It is taken from the earth's surface to a height h = 3 R when R is the radius of the earth. The change in gravitational potential energy of the body is