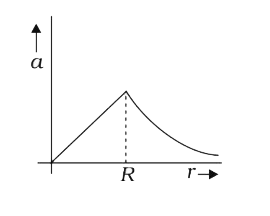
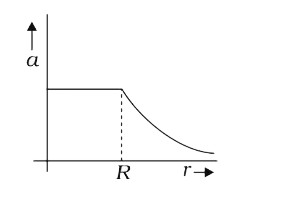
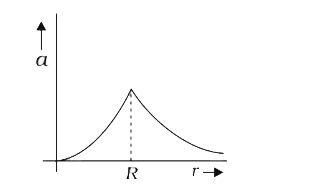
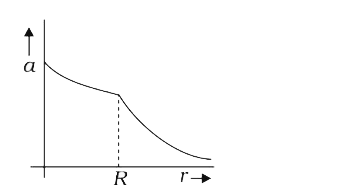
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The mass density of a spherical body is given by rho(r)=k/r for r le R...
Text Solution
|
- Let there be a spherically symmetric charge distribution with charge d...
Text Solution
|
- Consider a solid sphere oFIGURE radius R and mass density rho(r)=rho(0...
Text Solution
|
- Consider a spherical symmetric charge distribution with charge densi...
Text Solution
|
- [" Consider a spherical symmetric "],[" charge distribution with charg...
Text Solution
|
- The mass density of a spherical body is given by rho(r)=k/r for r le R...
Text Solution
|
- The volume charge density in a spherical ball of radius R varies with ...
Text Solution
|
- Let there be a spherical symmetric charge density varying as p(r )=p(0...
Text Solution
|
- Charge density of a sphere of radius R is rho = rho0/r where r is dist...
Text Solution
|