Home
Class 12
PHYSICS
A straight of length L extends from x=a ...

A straight of length L extends from x=a to x=L+a. the gravitational force it exerts on a point mass 'm' at x=0, if the mass per unit length of the rod is `A+Bx^(2), ` is given by :

A

`Gm[A(1/(a+L)-1/a)-BL]`

B

`Gm[A(1/a-1/a+L)-BL]`

C

`Gm[A(1/(a+L)-1/a)+BL]`

D

`Gm[A(1/a-1/(a+L))-BL]`

Text Solution

Verified by Experts

The correct Answer is:
B
`dm=rdx = (A+Bx^2)dx`
`F=int_(a)^(a+L) (GmDM)/x^2 =GM int_a^(a+L) ((A+Bx^2)dx)/x^2`
`=GM[int_a^(a+L) A/x^2 dx+a int_a^(a+L) Bdx]`
`F=4m[A(1/a-1/(a+L))]+BL " " =GM[A(L/(a(a+l)))+Bl]`
Promotional Banner

Similar Questions

Explore conceptually related problems

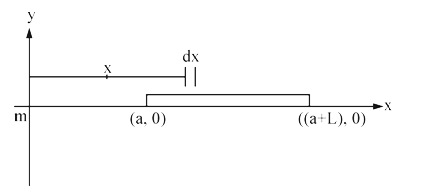
A straight rod of length L extends from x=a to x=L+a . Find the gravitational force exerts on a point mass m at x=0 is (if the linear density of rod mu=A+Bx^(2) )

A straight rod of length L has one of its end at the origin and the other at X=L . If the mass per unit length of the rod is given by Ax where A is constant, where is its centre of mass?

Find the gravitatinal force of between a point mass m placed at a disance x on the prolongation of a thin rod of mass M andlength l from near end .

Find the gravitational force between a point like mass M and an infinitely long, thin rod, of mass density rho , which is at a distance L from the mass M.

A straight rod of length 'l' extends from x=l to x=2l. If linear mass density of rod is mu=((mu_0)/(l^3)X^3) , then the gravitational force exerted by rod on a particle of mass m at x=0 , is

Find the potential energy of the gravitational interaction of a point mass m and a rod of mass m and length l , if they are along a straight line. Point mass is at a distance of a from the end of the rod. Find the potential energy of the gravitational

Find the potential energy of the gravitational interation of a point mass of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line such that the point mass is at a distance 'a' from one end. Also find the force of their interaction.

Calculate the force exerted by point mass m on rod of uniformly distributed mass M and length l (Placed as shown in figure) .

The gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length l and mass in as shown in figure is

A thin rod of mass M and length L is bent into a semicircle as shown in diagram. What is a gravitational force on a particle with mass m at the centre of curvature?