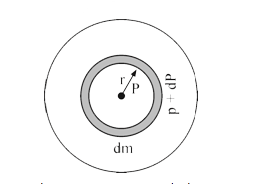
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A spherical body of radius R consists of a fluid of constant density a...
Text Solution
|
- A spherical body of radius R consists of a fluid of constant density a...
Text Solution
|
- Consider a spherical planet of radius R . Its density varies with the ...
Text Solution
|
- The volume charge density in a spherical ball of radius R varies with ...
Text Solution
|
- एक एकसमान घनत्व के तरल के गोलाकार पिण्ड की त्रिज्या R है तथा यह अपने स...
Text Solution
|
- एक गोले की त्रिज्या R तथा घनत्व rho है। इसे sigma घनत्व वाले द्रव में ...
Text Solution
|
- यदि गोलीय द्रव बूँद (पृष्ठ तनाव S) की त्रिज्या r से (r + Delta r) बढ़त...
Text Solution
|
- पृष्ठ तनाव S के द्रव में गैस के R त्रिज्या के बुलबुले में दाब आधिक्य...
Text Solution
|
- r त्रिज्या का एक गोलाकार पिण्ड की उत्सर्जित ऊर्जा P व शीतलन पर r है, त...
Text Solution
|