Home
Class 12
PHYSICS
Two satellites S1 and S2 revole round a ...

Two satellites `S_1 and S_2` revole round a planet in coplanar circular orbits in the same sanse. Their periods of revolution are 1 hour and 8 hour respectively. The radius of the orbit of `S_1 is 10^4 km,` When `S_2 is closest to S_1` find
(i) the speed of `S_2 relative to `S_1`
(ii) the angular speed of `S_2` as actually observed by an astronaut is `S_1.`

Text Solution

Verified by Experts

The correct Answer is:
(i)4 (ii
(i) According to Kepler’s third law
`Tpropr^(3//2)`
`T_1^2/T_2^2=R_1^3/R_2^3 rArr R_2^3=R_1^3 xx T_2^2/T_1^2 therefore R_2^3=10^12xx8^2/1^2=64xx10^12 rArr R_2=4xx10^4` km
The speed of satellite `S_1 V_1=(2piR_1)/T_1 =(2pixx10^4)/1` km/hr
The speed of satellite `S_2V_2=(2piR_2)/T_1=(2pixx4xx10^4)/8 = pixx10^4`
The speed of satellites `S_2` relative to `S_1`.

The speed of satellite `S_2V_2=(2piR_2)/T_1 = (2pixx4xx10^4)/8=pixx10^4`
The speed of satellites `S_2` relative to `S_1`.
`|V_(2.1)|=|V_2-V_1|=pixx10^4-2pixx10^4 = pixx10^4` km/hr
(ii) The angular speed of satellite `S_2` relative to `S_1`
`S_1=V_r/R_r =(|V_2-V_1|)/(R_2-R_1) =(pixx10^4)/((4xx10^(4)-10^4))=pi/3` rad/hr
Promotional Banner

Similar Questions

Explore conceptually related problems

Two satellites S_(1) and S_(2) resolve round a planet in coplaner circular orbit in the same sense. Their period of revolution are 1 hour and 8 hour respectively. The radius of the orbit of S_(1) is 10^(4) km . When S_(2) is closest to S_(1) , find (a) The speed of S_(2) relative to S_(1) , (b) The angular speed of S_(2) actually observed by an astronaut is S_(1)

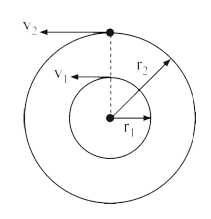
Two satellites S1 and S2 revolve round a planet in coplanar circular orbits in the same sense. TI1eir periods of revolution are 2 hours and 16 hours respectively. If the radius of the orbit of S_1 is 10^4 , then the radius of the orbit of S_2 is

Two satellite S_1 and S_2 revolve roudna planet in coplanar circular orbits in the same sense. Their periods of revoltions are 1 h nd 8 h respectively. tE radius of the orbit of S_1 is 10^4 km . When S_2 is closet to S_1 ., find as. The speed of S_2 relative to S_1 and b. the angular speed of S_2 as observed by an astronaut in S_1 .

Two satellite S_(1) and S_(2) revolve round a planet in coplanar circular orbits in the same sense. Their periods of revolution are 1hr and 8hours respectively. The radius of the orbit of S_(1) is 10^(4)km . When S_(2) is closet to S_(1) (i) the speed S_(2) relative to S_(1) as actually observed by an astronaut in S_(1) .

Two satellites S_(1) and S_(2) revolve around a planet in coplanar circular orbits in the same sense their periods of revolution are 1 hour and 8hours respectively the radius of the orbit of S_(1) is 10^(4) km when S_(1) is closest to S_(2) the angular speed of S_(2) as observed by an astronaut in S_(1) is :

Two saetllites S_(1) and S_(2) revolve around a planet in coplaner circular orbit in the same sense. Their periods of revolutions are 1 hour and 8 hours respectively. The radius of orbit of S_(1) is 10^(4) km . When S_(2) is closed to S_(1) , the speed of S_(2) relative to S_(1) is pi xx 10^(n) km//h . what is the value of n ?

Two satellites S_(1) and S_(2) revolve round a planet in the same direction in circular orbits. Their periods of revolutions are 1 hour and 8 hour respectively. The radius of S_(1) is 104 km. The velocity of S_(2) with respect to S_(1) will be -

Two stallites A and B revolve round the same planet in coplanar circular orbits lying in the same plane. Their periods of revolutions are 1h and 8h, respectively. The radius of the orbit of A is 10^(4) km. The speed of B relative to A when they are closed in kmh^(-1) is

In the above example the angular velocity of S_(2) as actually observed by an astronaut in S_(1) is -

S_(1) and S_(2) are two satellites revolving around a planet P in coplanar circular orbits in anticlockwise direction. Their period of revolution are 50 minutes and 400 minutes respectively. The radius of orbit of S_(2) is 5 xx 10^(4) km . (a) Find the radius of orbit of S_(1) (b) When S_(2) is closest to S_(1) , then find (i) speed of S_(1) relative to S_(2) and (ii) angular speed of S_(1) as observed by astronaut in S_(2) .