Home
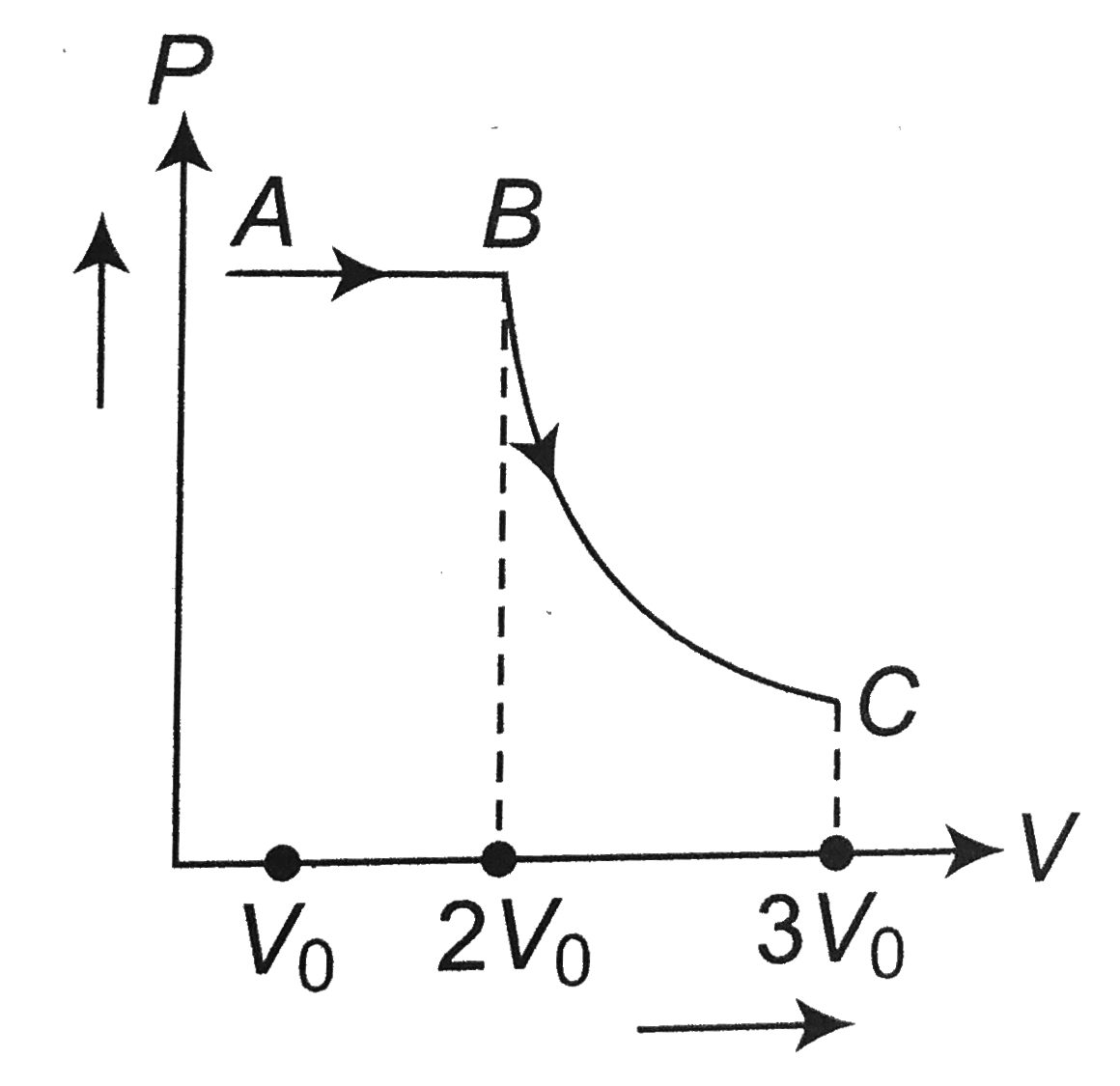
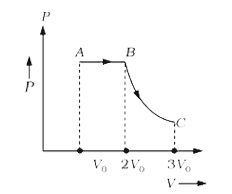
Class 12
PHYSICS
One mole of a gas is subjected to two pr...

One mole of a gas is subjected to two process AB and BC, one after the other as shown in the figure. BC is represented by `PV^(n) = constant`. We can conclude that (where T = temperature, W = work done by gas, V = volume and U = internal energy).

A

`T_A = T_B = T_C`

B

`V_A lt V_B , P_B le P_C`

C

`V_(AB) lt V_(AB)`

D

`U_A lt U_B`

Text Solution

Verified by Experts

The correct Answer is:
D
AB : Isobaric process
`V prop T`
`rArr T_B =2 T_A`
So `U_B = 2U _A`
` U_B gt U_A`
Or `U_A lt U_B`
Promotional Banner

Similar Questions

Explore conceptually related problems

One mole of an ideal diatomic gas is taken through a process whose P-V diagram is shown in the figure. The work done by the gas is

One mole of ideal gas undergoes a linear process as shown in figure below. Its temperature expressed as function of volume V is -

In the cyclic process shown in the figure, the work done by the gas in one cycle is

If one mole of gas doubles its volume at temperature T isothermally then work done by the gas is

One mole of a monoatomic gas is enclosed in a cylinder and occupies a volume of 4 liter at a pressure 100N//m^(2) . It is subjected to process T = = alphaV^(2) , where alpha is a positive constant , V is volume of the gas and T is kelvin temperature. Find the work done by gas (in joule) in increasing the volume of gas to six times initial volume .

One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure, The change in internal energy of the gas during the transition is :

Two moles of a monoatomic ideal gas undergoes a process AB as shown in the figure. Then, find the work done during the process in Joule.

One mole of an ideal monoatomic gas is taken along the path ABCA as shown in the PV diagram. The maximum temperature attained by the gas along the path BC is given by :

One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure The change to internal energy of the gas during the transition is