A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
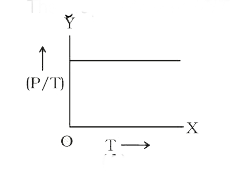
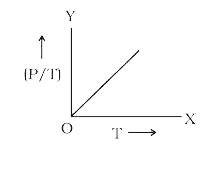
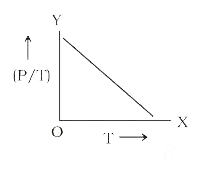
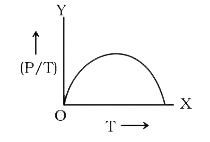
- The graph between (P/T) and T for a gas at constant volume will be:
Text Solution
|
- Straight line on (p - T) graph for an ideal gas represents isochoric p...
Text Solution
|
- The P-T graph for the given mass of an ideal gas is shown in figure. T...
Text Solution
|
- A plot of P vs T for a given mass of gas at constant volume is a strai...
Text Solution
|
- For a fixed mass of an ideal gas draw the following graphs: (i) P/T ...
Text Solution
|
- The graph between (P/T) and T for a gas at constant volume will be:
Text Solution
|
- The ideal gas equation for 1 mol of ideal gas is PV = nRT graph betw...
Text Solution
|
- Draw p-T graph for masses m and 2m of the same gas, when heated in a c...
Text Solution
|
- मोल आदर्श गैस के व्यवहार को एक वायुमण्डलीय दाब पर प्रदर्शित किया गया ह...
Text Solution
|