Home
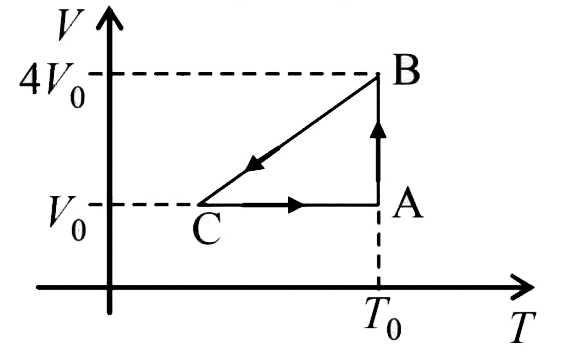
Class 12
PHYSICS
One mole of an ideal gas in initial stat...

One mole of an ideal gas in initial state A undergoes a cyclic process ABCA, as shown in the figure. Its pressure at A is `P_0`. Choose the correct option (s) from the following

A

Internal energies at A and B are the same

B

Work done by the gas in process AB is `P_0 V_0` in 4

C

Pressure at C is `P_0 //4`

D

Temperature at C is `T_0 //4`

Text Solution

Verified by Experts

The correct Answer is:
A, B
Process AB is isothermal. Temperature at A and B is the same, so internal energy at A and B is the same.
`Delta W_("AB" = nRT_0 "In" (V_B //V_A)`
For point `A : P_0 V_0 = nRT_0`
So `Delta W_(AB) = P_0 V_0 "In "= P_0 V_0 "In " (4 V_0 //V_0) = P_0 V_0 "In " (4)`
Nothing can be said about pressure and temperature at C.
Promotional Banner

Similar Questions

Explore conceptually related problems

One mole of an ideal gas in initial state A undergoes a cylic process ABCA, as shown in the figure. Its pressure at A is P_0 . Choose the correct option (s) from the following

One mole of an ideal monoatomatic gas is taken round the cylic process ABCA as shown Then

One mole of an ideal mono-atomic gas is taken round cyclic process ABCD as shown in figure below. Calculate

An ideal gas undergoes the cyclic process shown in a graph below :

An ideal monatomic gas undergoes a cyclic process ABCA as shown in the figure. Graph of pressure versus volume of the cyclic process ABCA is

One mole of an ideal monoatomic gas is taken through a cyclic process as shown. Choose the correct option(s).

2 moles of an ideal monoatomic gas undergoes a cyclic process ABCA as shown in the figure. R is the univers l gas constant. ("given ln 2"=0.693) Answer the following questions Graph of pressure versus volume of the cyclic process ABCA is

An ideal monoatomic gas undergoes a cyclic process ABCA as shown in the figure. The ratio of heat absorbed during AB to the work done on the gas during BC id

Two moles of a monatomic ideal gas undergo a cyclic process ABCDA as shown in figure. BCD is a semicircle. Find the efficiency of the cycle.