A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
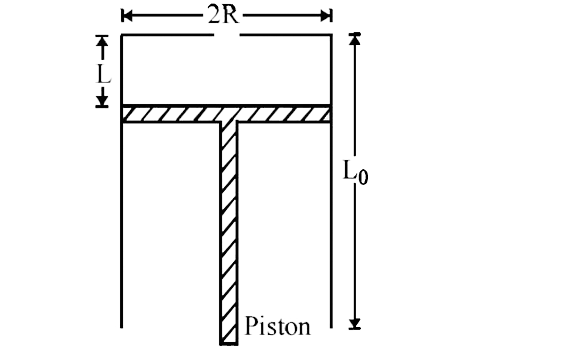
- A fixed thermally conducting cylinder has a radius R and height L0. Th...
Text Solution
|
- A fixed thermally conducting cylinder has a radius R and height L0. Th...
Text Solution
|
- A fixed thermally conducting cylinder has a radius R and height L0. Th...
Text Solution
|
- A fixed thermally conducting cylinder has a radius R and height L0. Th...
Text Solution
|
- A cylinder vessel containing a liquid of density rho is closed by a sm...
Text Solution
|
- There is a small hole in the bottom of a fixed container containing a ...
Text Solution
|
- The piston I s now pulled out slowly and held at a diatance 2L from th...
Text Solution
|
- While the piston is at a distance 2L from the top, the hole at the top...
Text Solution
|
- A fixed thermally conducting cylinder has radius R and length L0 . The...
Text Solution
|