Home
Class 12
PHYSICS
A small spherical monoatomic ideal gas b...

A small spherical monoatomic ideal gas bubble `(gamma=5//3)` is trapped inside a liquid of density `rho` (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is `T_0`, the height of the liquid is H and the atmospheric pressure `P_0` (Neglect surface tension).

As the bubble moves upwards, besides the buoyancy force the following forces are acting on it

A

`rho_l n Rg T_0 (P_0 + rho_l gH_^(2//5))/((P_0 + rho_l gy)^(7//5))`

B

`(rho_l n RgT_0)/((P_0 + rho_l gH)^(2//5)[(P_0 + rho_l (H-Y))]^(3//5))`

C

`rho_l nRgT_0 ((P_0 + rho_l gH)^(3//5))/((P_0 + rho_l gy)^(8//5))`

D

`(rho_l nRgT_0)/((P_0 + rho_l gH)^(3//5)[P_0 + rho_l g(H - Y)]^(2//5))`

Text Solution

Verified by Experts

The correct Answer is:
B
`F_B = rho_1 g` (Volume of bubble)
Volume can be calculated by
`PV^(gamma)` = Const
`((P_0 + rho_1 g(H-Y))/(P_0 + rho_1 gH))(V/V_0)^(5//3)=1 " "rArr" "V=V_0((P_0+rho_1 gH)/(P_0 + rho_1 g (H-y)))^(3//5)`
So, `F_B = (nRT_0 rho_1 g)/((P_(0)+rho_1 gH)^(2//5)(P_0 + rho_1g(H-Y))^(3//5))`
Promotional Banner

Similar Questions

Explore conceptually related problems

A small spherical monoatomic ideal gas bubble (gamma=5//3) is trapped inside a liquid of density rho (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T_0 , the height of the liquid is H and the atmospheric pressure P_0 (Neglect surface tension). When the gas bubble is at a height y from the bottom, its temperature is-

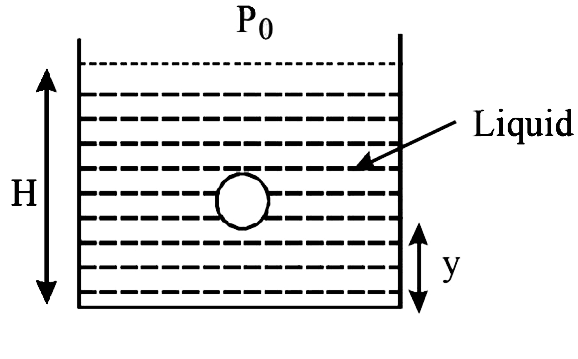
A small spherical monoatomic ideal gas bubble (gamma=5//3) is trapped inside a liquid of density rho (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T_0 , the height of the liquid is H and the atmospheric pressure P_0 (Neglect surface tension). The buyoncy force acting on the gas bubble is (Assume R is the universal gas constant)

A small spherical monoatomic ideal gas bubble (gamma= (5)/(3)) is trapped inside a liquid of density rho_(l) (see figure) . Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T_(0) , the height of the liquid is H and the atmospheric pressure is P_(0) (Neglect surface tension). When the gas bubble is at a height y from the bottom , its temperature is :-

At the boiling point , bubbles form within the liquid because

An air bubble is formed at depth h below the surface of water. The pressure inside the bubble is- ( P_(0)= atmospheric pressure, r = radius of bubble)

A small air bubble of radius r in water is at depth h below the water surface. If P_0 is the atmospheric pressure, rho is the density of water and T is the surface tension of water, what is the pressure inside the bubble?

The gas inside a spherical bubble expands uniformly and slowly so that its radius increases from R to 2R . Let the atmospheric pressure be p_(0) and surface tension be S . The work done by the gas in the process is

A small air bubble of radius r in water is at a depth h ( r lt lt h ) . If P_(o) is the atmospheric pressure, rho is the density of water and T is the surface tension of water, the excess pressure inside the bubble over the pressure outside it is

Two spherical bubbles of radii 3 cm and 4cm coalesce to form another spherical bubble. Calculate the surface tension of the bubble. The radius of the bubble formed=4.498 cm and the atmopheric pressure =10^(5) Pa