Home
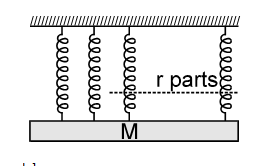
Class 12
PHYSICS
A spring of spring constant k is cut int...

A spring of spring constant k is cut into n equal parts, out of which r parts are placed in parallel and connected with mass M as shown in figure. The time period of oscillatory motion of mass M is:

A

`T=2pisqrt((M)/(rnK))`

B

`T=2pisqrt((nrM)/(K))`

C

`T=2pisqrt((nM)/(nK))`

D

`T=2pisqrt((nM)/(rK))`

Text Solution

Verified by Experts

The correct Answer is:
A
`K.I=k'xx(I)/(n)` constant
new spring constand for each part is k'=nK
Now r part are taken in parallel.
so `K_(eq)=nrk`, Time period =`2pisqrt((M)/(K_(eq)))=2pisqrt((M)/(nrK))`
Promotional Banner

Similar Questions

Explore conceptually related problems

A spring of spring constant K is cut equal parts of which t part are places in particle and connected will mass m shown in figure The time period of oscilation motion of mass m is

A spring of spring constant k is cut in three equal pieces. The spring constant of each part will be

A spring of force constant k is cut into four equal parts. The force constant of each part will be

A spring of force constant k is cut into there equal part what is force constant of each part ?

A spring (spring constant=k) is cuttend into 4 equal parts and two parts are connected in parallel. What is the effective spring constant?

A spring is of spring constant k=15 N//cm . It is cut into 3 equal parts, which are joined in parallel. What is the spring constant of the combination ?

A spring of force constant 20 N/m is cut into four equal parts, All the four parts are now connected in parallel. Find the force constant of the combination.