A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
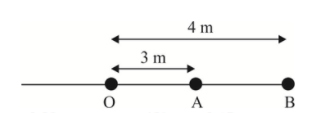
- A particle is performing SHM about mean position O as shown in the fig...
Text Solution
|
- A particle executes SHM with a time period of 4 s . Find the time take...
Text Solution
|
- A particle starts from a point P at a distance of A//2 from the mean p...
Text Solution
|
- A particle starts from a point P at a distance of A//2 from the mean ...
Text Solution
|
- A particle executing SHM of amplitude 4 cm and T=4 s .The time taken b...
Text Solution
|
- A particle executes SHM with a time period of 4 s . Find the time take...
Text Solution
|
- A particle is executing SHM with time period T Starting from mean posi...
Text Solution
|
- A particle is performing SHM about mean position O as shown in the fig...
Text Solution
|
- A particle executes SHM with a time period of 12s. Find the time taken...
Text Solution
|